---
license: cc-by-nc-4.0
language:
- en
pipeline_tag: text-generation
tags:
- nvidia
- AceMath
- math
- pytorch
---
## Introduction
We introduce AceMath, a family of frontier models designed for mathematical reasoning. The models in AceMath family, including AceMath-1.5B/7B/72B-Instruct and AceMath-7B/72B-RM, are Improved using Qwen.
The AceMath-1.5B/7B/72B-Instruct models excel at solving English mathematical problems using Chain-of-Thought (CoT) reasoning, while the AceMath-7B/72B-RM models, as outcome reward models, specialize in evaluating and scoring mathematical solutions.
The AceMath-1.5B/7B/72B-Instruct models are developed from the Qwen2.5-Math-1.5B/7B/72B-Base models, leveraging a multi-stage supervised fine-tuning (SFT) process: first with general-purpose SFT data, followed by math-specific SFT data. We are releasing all training data to support further research in this field.
For more information about AceMath, check our [website](https://research.nvidia.com/labs/adlr/acemath/) and [paper](https://arxiv.org/abs/2412.15084).
## All Resources
[AceMath-1.5B-Instruct](https://huggingface.co/nvidia/AceMath-1.5B-Instruct) [AceMath-7B-Instruct](https://huggingface.co/nvidia/AceMath-7B-Instruct) [AceMath-72B-Instruct](https://huggingface.co/nvidia/AceMath-72B-Instruct)
[AceMath-7B-RM](https://huggingface.co/nvidia/AceMath-7B-RM) [AceMath-72B-RM](https://huggingface.co/nvidia/AceMath-72B-RM)
[AceMath-Instruct Training Data](https://huggingface.co/datasets/nvidia/AceMath-Instruct-Training-Data) [AceMath-RM Training Data](https://huggingface.co/datasets/nvidia/AceMath-RM-Training-Data)
[AceMath-RewardBench](https://huggingface.co/datasets/nvidia/AceMath-RewardBench) [AceMath Evaluation Script](https://huggingface.co/datasets/nvidia/AceMath-RewardBench/tree/main/scripts)
## Benchmark Results
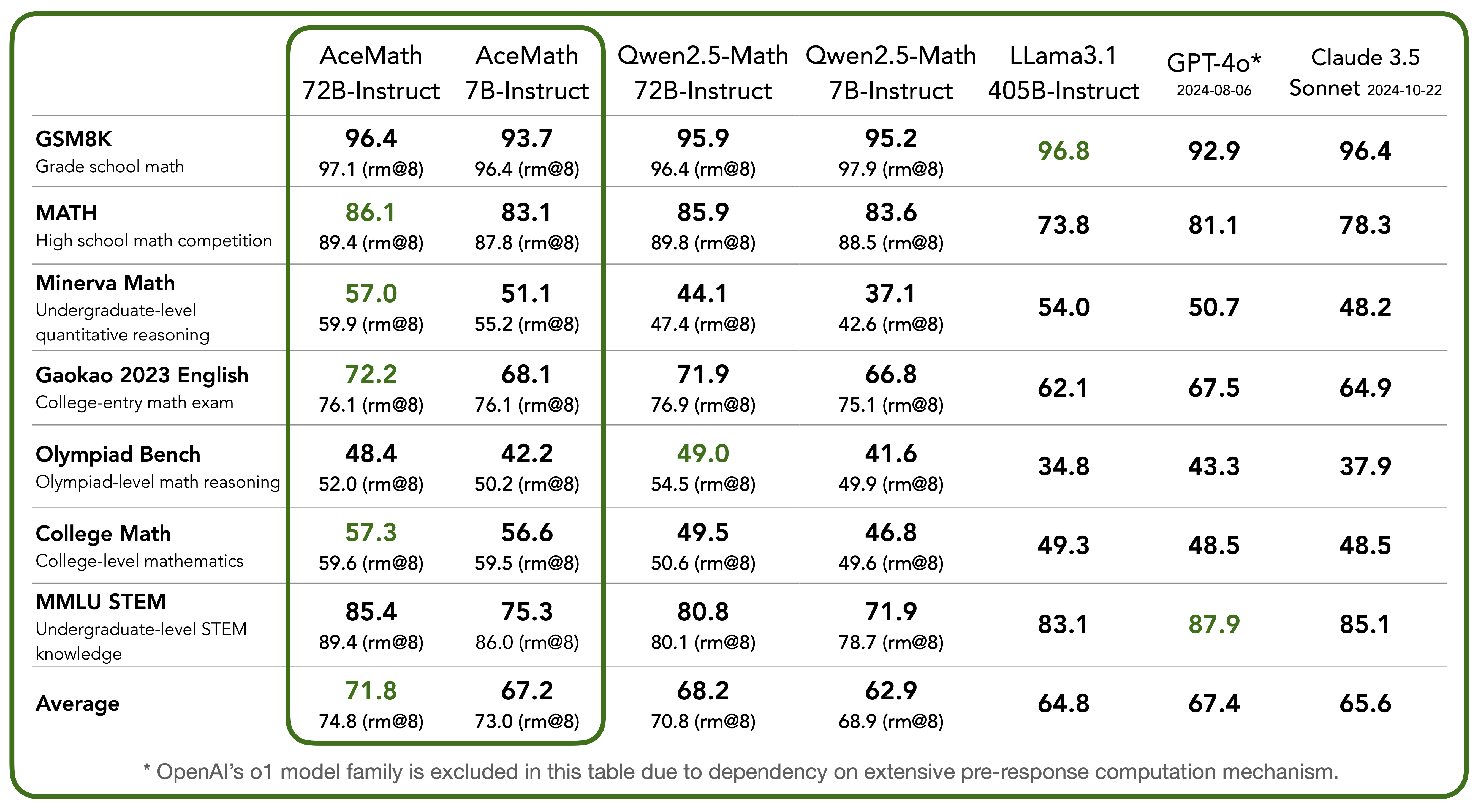
Greedy decoding (pass@1) results on a variety of math reasoning benchmarks. AceMath-7B-Instruct significantly outperforms the previous best-in-class Qwen2.5-Math-7B-Instruct (67.2 vs. 62.9) and comes close to the performance of 10× larger Qwen2.5-Math-72B-Instruct (67.2 vs. 68.2). Notably, our AceMath-72B-Instruct outperforms the state-of-the-art Qwen2.5-Math-72B-Instruct (71.8 vs. 68.2), GPT-4o (67.4) and Claude 3.5 Sonnet (65.6) by a margin.
## How to use
```python
import torch
from transformers import AutoModelForSequenceClassification, AutoTokenizer
model_name = "nvidia/AceMath-7B-RM" # Path to the model
device = "auto" # the device to load the model onto
model = AutoModelForSequenceClassification.from_pretrained(
model_name,
device_map=device,
num_labels=1,
torch_dtype=torch.bfloat16,
trust_remote_code=True,
).eval()
tokenizer = AutoTokenizer.from_pretrained(model_name, trust_remote_code=True)
prompt = """Compute
\[\sum_{n = 1}^\infty \frac{F_{n + 1}}{F_n F_{n + 2}},\]where $F_n$ denotes the $n$th Fibonacci number, so $F_0 = 0$ and $F_1 = 1.$"""
resp_1 = """To compute \[\sum_{n=1}^\infty \frac{F_{n+1}}{F_n F_{n+2}},\] where \( F_n \) is the \(n\)-th Fibonacci number, we will use the recurrence relation \( F_{n+2} = F_{n+1} + F_n \) and properties of Fibonacci numbers.\n\n---\n\n### Step 1: Simplify the General Term\n\nThe given term is\n\[\frac{F_{n+1}}{F_n F_{n+2}}.\]\n\nUsing the Fibonacci recurrence relation \( F_{n+2} = F_{n+1} + F_n \), we rewrite \( \frac{1}{F_{n+2}} \) as\n\[\frac{1}{F_{n+2}} = \frac{1}{F_{n+1} + F_n}.\]\n\nThus, the term becomes\n\[\frac{F_{n+1}}{F_n F_{n+2}} = \frac{F_{n+1}}{F_n (F_{n+1} + F_n)}.\]\n\nNow, separate the fraction into partial fractions:\n\[\frac{F_{n+1}}{F_n (F_{n+1} + F_n)} = \frac{1}{F_n} - \frac{1}{F_{n+1}}.\]\n\n---\n\n### Step 2: Write the Series\n\nThe series becomes\n\[\sum_{n=1}^\infty \frac{F_{n+1}}{F_n F_{n+2}} = \sum_{n=1}^\infty \left( \frac{1}{F_n} - \frac{1}{F_{n+1}} \right).\]\n\nThis is a **telescoping series**, where most terms cancel out. Writing the first few terms explicitly:\n\[\sum_{n=1}^\infty \left( \frac{1}{F_n} - \frac{1}{F_{n+1}} \right) = \left( \frac{1}{F_1} - \frac{1}{F_2} \right) + \left( \frac{1}{F_2} - \frac{1}{F_3} \right) + \left( \frac{1}{F_3} - \frac{1}{F_4} \right) + \cdots.\]\n\nAll intermediate terms cancel, leaving:\n\[\frac{1}{F_1} - \lim_{n \to \infty} \frac{1}{F_{n+1}}.\]\n\n---\n\n### Step 3: Evaluate the Remaining Terms\n\n- The first Fibonacci number \( F_1 = 1 \), so \( \frac{1}{F_1} = 1 \).\n- As \( n \to \infty \), \( F_{n+1} \to \infty \), so \( \frac{1}{F_{n+1}} \to 0 \).\n\nThus, the sum is:\n\[\sum_{n=1}^\infty \frac{F_{n+1}}{F_n F_{n+2}} = 1 - 0 = 1.\]\n\n---\n\n### Final Answer:\n\n\[\boxed{1}\]"""
chat = [
{"role": "system", "content": "Please reason step by step, and check your final answer within \\boxed{}."},
{"role": "user", "content": prompt},
{"role": "assistant", "content": resp_1}
]
conversation_str = tokenizer.apply_chat_template(
chat,
tokenize=False,
add_generation_prompt=False
)
input_ids = tokenizer.encode(
conversation_str,
return_tensors="pt",
add_special_tokens=False
).to(model.device)
outputs = model(input_ids=input_ids)
print(outputs[0][0])
```
## Correspondence to
Zihan Liu (zihanl@nvidia.com), Yang Chen (yachen@nvidia.com), Wei Ping (wping@nvidia.com)
## Citation
If you find our work helpful, we’d appreciate it if you could cite us.
@article{acemath2024,
title={AceMath: Advancing Frontier Math Reasoning with Post-Training and Reward Modeling},
author={Liu, Zihan and Chen, Yang and Shoeybi, Mohammad and Catanzaro, Bryan and Ping, Wei},
journal={arXiv preprint},
year={2024}
}
## License
All models in the AceMath family are for non-commercial use only, subject to [Terms of Use](https://openai.com/policies/row-terms-of-use/) of the data generated by OpenAI. We put the AceMath models under the license of [Creative Commons Attribution: Non-Commercial 4.0 International](https://spdx.org/licenses/CC-BY-NC-4.0).

