Spaces:
Running
Running
add notes
Browse files- dist/assets/images/5Dparallelism_8Bmemoryusage.svg +0 -0
- dist/assets/images/activationrecomputation_memory.svg +2029 -0
- dist/assets/images/cp_70bmemoryusage.svg +2424 -0
- dist/assets/images/cp_8Bmemoryusage.svg +2334 -0
- dist/assets/images/cp_attnmask.svg +0 -0
- dist/assets/images/cp_memoryusage.svg +2334 -0
- dist/assets/images/cp_overlap_all2all.svg +221 -0
- dist/assets/images/cp_overlap_allgather.svg +185 -0
- dist/assets/images/cp_zigzagmask.svg +0 -0
- dist/assets/images/diving_primergpu.svg +0 -0
- dist/assets/images/diving_primergpu2.svg +0 -0
- dist/assets/images/dp_ourjourney_memoryusage.svg +2256 -0
- dist/assets/images/dp_overlap1.svg +364 -0
- dist/assets/images/dp_overlap2.svg +670 -0
- dist/assets/images/dp_overlap3.svg +400 -0
- dist/assets/images/dp_scaling.svg +1976 -0
- dist/assets/images/dp_zero1.gif +0 -0
- dist/assets/images/dp_zero1_overlap.svg +451 -0
- dist/assets/images/dp_zero2.gif +0 -0
- dist/assets/images/dp_zero2_overlap.svg +451 -0
- dist/assets/images/dp_zero3_bwd.svg +0 -0
- dist/assets/images/dp_zero3_fwd.svg +0 -0
- dist/assets/images/dp_zero3_overlap.svg +517 -0
- dist/assets/images/fp8_training_loss_curves.svg +0 -0
- dist/assets/images/memory_profile.svg +0 -0
- dist/assets/images/memusage_activations.svg +2353 -0
- dist/assets/images/pp_1f1b.svg +0 -0
- dist/assets/images/pp_1f1b_interleaved.svg +0 -0
- dist/assets/images/pp_afab.svg +827 -0
- dist/assets/images/pp_afab2.svg +0 -0
- dist/assets/images/pp_comm_bandwidth.svg +1479 -0
- dist/assets/images/pp_memoryusage.svg +1632 -0
- dist/assets/images/tp_memoryusage.svg +1963 -0
- dist/assets/images/tp_overlap.svg +251 -0
- dist/assets/images/tp_scaling.svg +1958 -0
- dist/assets/images/tp_sp_memoryusage.svg +2151 -0
- dist/assets/images/tp_sp_overlap.svg +309 -0
- dist/assets/images/tp_sp_scaling.svg +1898 -0
- dist/assets/images/what_we_learnt_heatmap copy.svg +0 -0
- dist/assets/images/what_we_learnt_heatmap.svg +0 -0
- dist/assets/images/what_we_learnt_parallel_coordinates.html +0 -0
- dist/assets/images/what_we_learnt_parallel_coordinates.svg +0 -0
- dist/assets/images/zero3_memoryusage.svg +2333 -0
- dist/assets/images/zero_memory.svg +0 -0
- dist/index.html +103 -38
- dist/style.css +35 -0
- src/index.html +103 -38
- src/style.css +35 -0
dist/assets/images/5Dparallelism_8Bmemoryusage.svg
ADDED

|
dist/assets/images/activationrecomputation_memory.svg
ADDED

|
dist/assets/images/cp_70bmemoryusage.svg
ADDED

|
dist/assets/images/cp_8Bmemoryusage.svg
ADDED

|
dist/assets/images/cp_attnmask.svg
ADDED

|
dist/assets/images/cp_memoryusage.svg
ADDED

|
dist/assets/images/cp_overlap_all2all.svg
ADDED

|
dist/assets/images/cp_overlap_allgather.svg
ADDED

|
dist/assets/images/cp_zigzagmask.svg
ADDED

|
dist/assets/images/diving_primergpu.svg
ADDED

|
dist/assets/images/diving_primergpu2.svg
ADDED

|
dist/assets/images/dp_ourjourney_memoryusage.svg
ADDED

|
dist/assets/images/dp_overlap1.svg
ADDED

|
dist/assets/images/dp_overlap2.svg
ADDED

|
dist/assets/images/dp_overlap3.svg
ADDED

|
dist/assets/images/dp_scaling.svg
ADDED

|
dist/assets/images/dp_zero1.gif
ADDED
|
dist/assets/images/dp_zero1_overlap.svg
ADDED

|
dist/assets/images/dp_zero2.gif
ADDED
|
dist/assets/images/dp_zero2_overlap.svg
ADDED

|
dist/assets/images/dp_zero3_bwd.svg
ADDED

|
dist/assets/images/dp_zero3_fwd.svg
ADDED

|
dist/assets/images/dp_zero3_overlap.svg
ADDED

|
dist/assets/images/fp8_training_loss_curves.svg
ADDED

|
dist/assets/images/memory_profile.svg
ADDED

|
dist/assets/images/memusage_activations.svg
ADDED

|
dist/assets/images/pp_1f1b.svg
ADDED

|
dist/assets/images/pp_1f1b_interleaved.svg
ADDED

|
dist/assets/images/pp_afab.svg
ADDED

|
dist/assets/images/pp_afab2.svg
ADDED

|
dist/assets/images/pp_comm_bandwidth.svg
ADDED

|
dist/assets/images/pp_memoryusage.svg
ADDED

|
dist/assets/images/tp_memoryusage.svg
ADDED

|
dist/assets/images/tp_overlap.svg
ADDED

|
dist/assets/images/tp_scaling.svg
ADDED

|
dist/assets/images/tp_sp_memoryusage.svg
ADDED

|
dist/assets/images/tp_sp_overlap.svg
ADDED

|
dist/assets/images/tp_sp_scaling.svg
ADDED

|
dist/assets/images/what_we_learnt_heatmap copy.svg
ADDED

|
dist/assets/images/what_we_learnt_heatmap.svg
ADDED

|
dist/assets/images/what_we_learnt_parallel_coordinates.html
ADDED
|
The diff for this file is too large to render.
See raw diff
|
|
|
dist/assets/images/what_we_learnt_parallel_coordinates.svg
ADDED

|
dist/assets/images/zero3_memoryusage.svg
ADDED

|
dist/assets/images/zero_memory.svg
ADDED

|
dist/index.html
CHANGED
|
@@ -222,11 +222,11 @@
|
|
| 222 |
<li>an optimization step using the gradients to update the parameters</li>
|
| 223 |
</ol>
|
| 224 |
|
|
|
|
|
|
|
| 225 |
<p>It looks generally like this: </p>
|
| 226 |
<p><img alt="image.png" src="assets/images/placeholder.png" /></p>
|
| 227 |
|
| 228 |
-
<aside>As we’ll see later, these steps may be repeated or intertwined but for now we’ll start simple.</aside>
|
| 229 |
-
|
| 230 |
<p>In this figure, the boxes on the top line can be seen as successive layers inside a model (same for the last line). The red boxes are the associated gradients for each of these layers, computed during the backward pass.</p>
|
| 231 |
|
| 232 |
<p>The batch size (<d-math>bs</d-math>) is one of the important hyper-parameters for model training and affects both model convergence and throughput.</p>
|
|
@@ -241,13 +241,12 @@
|
|
| 241 |
|
| 242 |
<p>In the simplest case, training on a single machine, the <d-math>bs</d-math> (in samples) and <d-math>bst</d-math> can be computed from the model input sequence length (seq) as follows :</p>
|
| 243 |
|
| 244 |
-
<aside><p>From here onward we’ll show the formulas for the batch size in terms of samples but you can always get its token-unit counterpart by multiplying it with the sequence length.
|
| 245 |
-
</aside>
|
| 246 |
-
|
| 247 |
<d-math block>
|
| 248 |
bst=bs *seq
|
| 249 |
</d-math>
|
| 250 |
|
|
|
|
|
|
|
| 251 |
<p>A sweet spot for recent LLM training is typically on the order of 4-60 million tokens per batch. However, a typical issue when scaling the training of our model to these large batch sizes is out-of-memory issues, ie. our GPU doesn’t have enough memory.</p>
|
| 252 |
|
| 253 |
<aside>Note: Llama 1 was trained with a batch size of ~4M tokens for 1.4 trillions tokens while DeepSeek was trained with a batch size of ~60M tokens for 14 trillion tokens.
|
|
@@ -267,13 +266,18 @@
|
|
| 267 |
<li>Model gradients</li>
|
| 268 |
<li>Optimizer states</li>
|
| 269 |
</ul>
|
| 270 |
-
|
| 271 |
-
<
|
|
|
|
|
|
|
|
|
|
| 272 |
<ul>
|
| 273 |
<li>CUDA Kernels typically require 1-2 GB of GPU memory, which you can quickly verify by running <code>import torch; torch.ones((1, 1)).to("cuda")</code> and then checking the GPU memory with <code>nvidia-smi</code>.</li>
|
| 274 |
<li>Some rest memory usage from buffers, intermediate results and some memory that can’t be used due to fragmentation</li>
|
| 275 |
</ul>
|
| 276 |
-
We’ll neglect these last two contributors as they are typically small and constant factors
|
|
|
|
|
|
|
| 277 |
|
| 278 |
<p>These items are stored as tensors which come in different <em>shapes</em> and <em>precisions</em>. The <em>shapes</em> are determined by hyper-parameters such as batch size, sequence length, model hidden dimensions, attention heads, vocabulary size, and potential model sharding as we’ll see later. <em>Precision</em> refers to formats like FP32, BF16, or FP8, which respectively require 4, 2, or 1 byte to store each single value in the tensor.</p>
|
| 279 |
|
|
@@ -328,13 +332,18 @@
|
|
| 328 |
\begin{aligned}
|
| 329 |
& m_{params} = 2 * N \\
|
| 330 |
& m_{grad} = 2 * N \\
|
| 331 |
-
& m_{
|
| 332 |
& m_{opt} = (4+4) * N
|
| 333 |
\end{aligned}
|
| 334 |
</d-math>
|
| 335 |
|
| 336 |
-
<
|
| 337 |
-
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 338 |
|
| 339 |
<p>Interestingly, mixed precision itself doesn’t save overall memory as it just distributes the memory differently across the three components, and in fact adds another 4 bytes over full precision training if we accumulate gradients in FP32. It’s still advantageous as having the model which does the forward/backward in half precision it allows us to (1) use optimized lower precision operations on the GPU which are faster and (2) reduces the activation memory requirements during the forward pass.</p>
|
| 340 |
|
|
@@ -422,9 +431,20 @@
|
|
| 422 |
|
| 423 |
<p><img alt="llama-8b-memory-bars--recomp.png" src="/assets/images/placeholder.png" /></p>
|
| 424 |
|
| 425 |
-
<
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 426 |
|
| 427 |
-
<aside
|
| 428 |
|
| 429 |
<p>Most training frameworks these days use FlashAttention (which we’ll cover a bit later) which integrate natively activation recomputation in its optimization strategy by recomputing attention scores and matrices in the backward pass instead of storing them. Thus most people using Flash Attention are already making use of selective recomputation.</p>
|
| 430 |
|
|
@@ -456,10 +476,11 @@
|
|
| 456 |
|
| 457 |
<p><img alt="image.png" src="/assets/images/placeholder.png" /></p>
|
| 458 |
|
| 459 |
-
<p><strong>Gradient accumulation allows us to reduce memory of activations which grow linearly with batch size by computing only only partial, micro-batches. There is a small overhead caused by the additional forward and backward passes.</strong></p>
|
| 460 |
-
|
| 461 |
<aside>Using gradient accumulation means we need to keep buffers where we accumulate gradients which persist throughout a training step. Whereas without gradient accumulation, in the backward gradients are computed while freeing the activations memory, which means a lower peak memory.</aside>
|
| 462 |
|
|
|
|
|
|
|
|
|
|
| 463 |
<p>But if you’ve carefully followed, you probably noticed that the forward/backward passes for each micro-batch can actually be run in parallel. Forward/backward passes are independent from each other, with independent input samples being the only difference. Seems like it’s time to start extending our training to more than one GPU! </p>
|
| 464 |
|
| 465 |
<p>Let’s get a larger workstation 🖥️ with a couple of GPUs and start investigating our first scaling technique called <em><strong>data parallelism</strong> which is just a parallel version of gradient accumulation</em>.</p>
|
|
@@ -548,7 +569,14 @@
|
|
| 548 |
|
| 549 |
<p>In PyTorch, this is typically solved by adding a <a href="https://github.com/pytorch/pytorch/blob/5ea67778619c31b13644914deef709199052ee55/torch/nn/parallel/distributed.py#L1408-L1435"><code>model.no_sync()</code></a> decorator, which disables gradient synchronization, on the backward passes which don’t need reduction.</p>
|
| 550 |
|
| 551 |
-
<
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 552 |
|
| 553 |
<h3>Revisit global batch size</h3>
|
| 554 |
<p>Let’s update our batch size equation with our newly learned Data Parallelism and Gradient Accumulation parameters:</p>
|
|
@@ -575,17 +603,19 @@
|
|
| 575 |
<li>Finally, we determine the number of available GPUs for our target DP. The ratio of GBS to DP gives us the remaining number of gradient accumulation steps needed for the desired GBS. </li>
|
| 576 |
</ol>
|
| 577 |
|
| 578 |
-
<aside>For instance DeepSeek and Llama models are trained with a 4k tokens sequence length during the main pretraining phase.</aside>
|
| 579 |
|
| 580 |
-
<aside>The reason 2-8k work well for pretraining is that documents that are longer are very rare on the web. See this <a href="https://www.harmdevries.com/post/context-length/">Harm’s blogpost</a> for a detailed analysis.
|
| 581 |
-
</aside>
|
| 582 |
|
| 583 |
<p>If the gradient accumulation ratio is lower than one, i.e. we have too many GPUs a.k.a GPU-rich 🤑 (!), we can either choose to not use all our GPUs, explore a larger global batch size or test if a lower MBS will speed up training. In the latter case we’ll end up prioritizing throughput over individual GPU compute efficiency, using a smaller MBS than possible in order to speed up training.</p>
|
| 584 |
|
| 585 |
<p>Time to take a concrete example: Let’s say we want to train a recent model with a GBS of 4M tokens and a sequence length of 4k. This means our batch size will be 1024 samples (we pick powers of two). We observe that a single GPU can only fit MBS=2 in memory and we have 128 GPUs available for training. This means with 4 gradient accumulation steps we’ll achieve our goal of 1024 samples or 4M tokens per training step. Now what if we suddenly have 512 GPUs available? We can achieve the same GBS and thus identical training by keeping MBS=2 and setting gradient accumulation steps to 1 and achieve faster training!</p>
|
| 586 |
|
| 587 |
-
<
|
| 588 |
-
|
|
|
|
|
|
|
|
|
|
|
|
|
| 589 |
|
| 590 |
<p>While data parallelism cleverly overlaps the all-reduce gradient synchronization with backward computation to save time, this benefit starts to break down at large scales. As we add more and more GPUs (hundreds or thousands), the overhead of coordinating between them grows significantly. The end result? We get less and less efficient returns from each additional GPU we add to the system:</p>
|
| 591 |
|
|
@@ -610,10 +640,10 @@
|
|
| 610 |
|
| 611 |
<p>In this section we will introduce DeepSpeed ZeRO (<strong>Ze</strong>ro <strong>R</strong>edundancy <strong>O</strong>ptimizer), a memory optimization technology designed to reduce memory redundancies in LLM training.</p>
|
| 612 |
|
| 613 |
-
<aside>We’ll focus on ZeRO-1 to ZeRO-3 in this blog as it should give a broad view on how it helps reduce memory while showing the tradeoffs to take into account. You can find more ZeRO flavors in the <a href="https://www.deepspeed.ai/tutorials/zero/">DeepSpeed docs</a>.</aside>
|
| 614 |
-
|
| 615 |
<p>While Data Parallelism is very efficient in scaling training, the naive replication of optimizer states, gradients, and parameters across each DP rank introduces a significant memory redundancy. ZeRO eliminates memory redundancy by partitioning the optimizer states, gradients, and parameters across the data parallel dimension, while still allowing computation with the full set of parameters. This sometimes requires more communications between DP ranks which may or may not be fully overlapped as we’ll see next!</p>
|
| 616 |
|
|
|
|
|
|
|
| 617 |
<p>This approach is organized into three possible optimization stage of ZeRO:</p>
|
| 618 |
|
| 619 |
<ul>
|
|
@@ -622,10 +652,10 @@
|
|
| 622 |
<li>ZeRO-3 (also called FSDP for “Fully-Sharded Data Parallelism”): optimizer state + gradient + parameter partitioning</li>
|
| 623 |
</ul>
|
| 624 |
|
| 625 |
-
<p>You might be missing the activations among the things we can shard. Since each DP replica of the model receives a different micro-batch the activations on each DP rank also differ so they are not duplicated and thus can’t be sharded!</p>
|
| 626 |
-
|
| 627 |
<aside>When we say partitioning, it means alongside the DP axis, as ZeRO is part of Data Parallelism. We’ll see later that we can partition alongside other axes.</aside>
|
| 628 |
|
|
|
|
|
|
|
| 629 |
<p>Let’s have a closer look how much we can save with the partitioning of each ZeRO stage!</p>
|
| 630 |
|
| 631 |
<h4>Memory usage revisited</h4>
|
|
@@ -639,7 +669,6 @@
|
|
| 639 |
<li>- Model’s gradients in fp32: <d-math>4\Psi</d-math> (optional, only accounted if we want to accumulate grads in fp32)</li>
|
| 640 |
</ul>
|
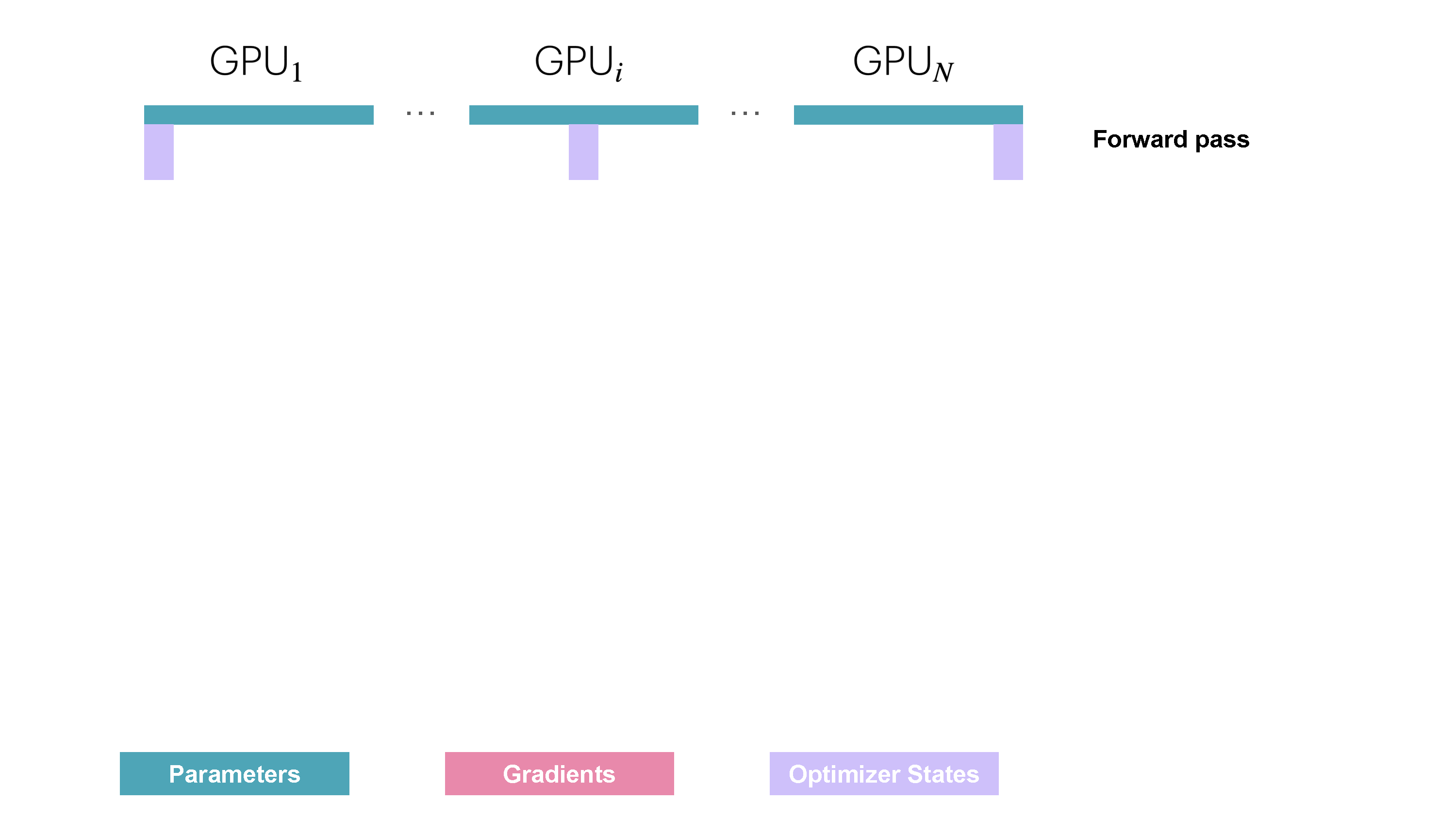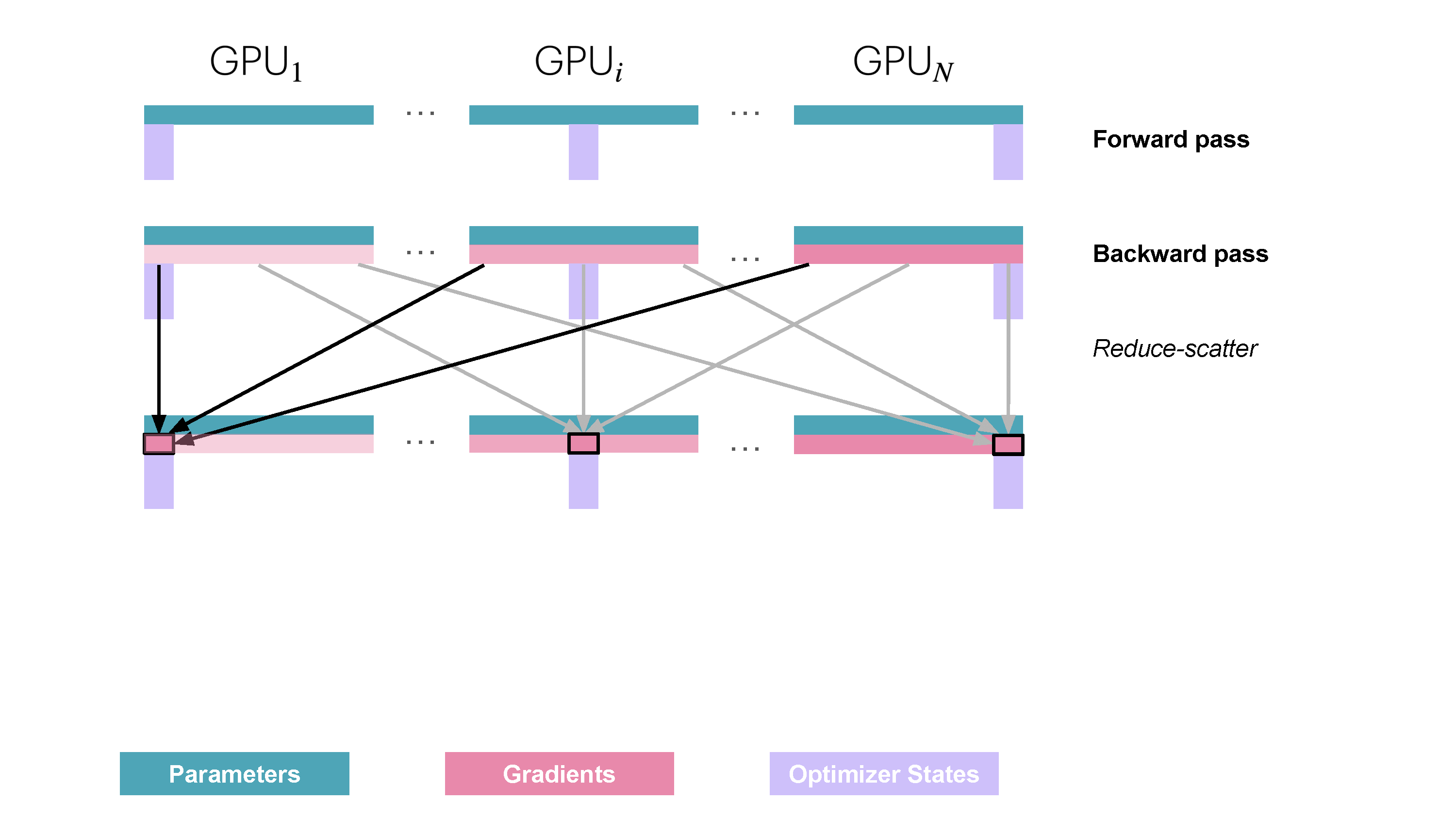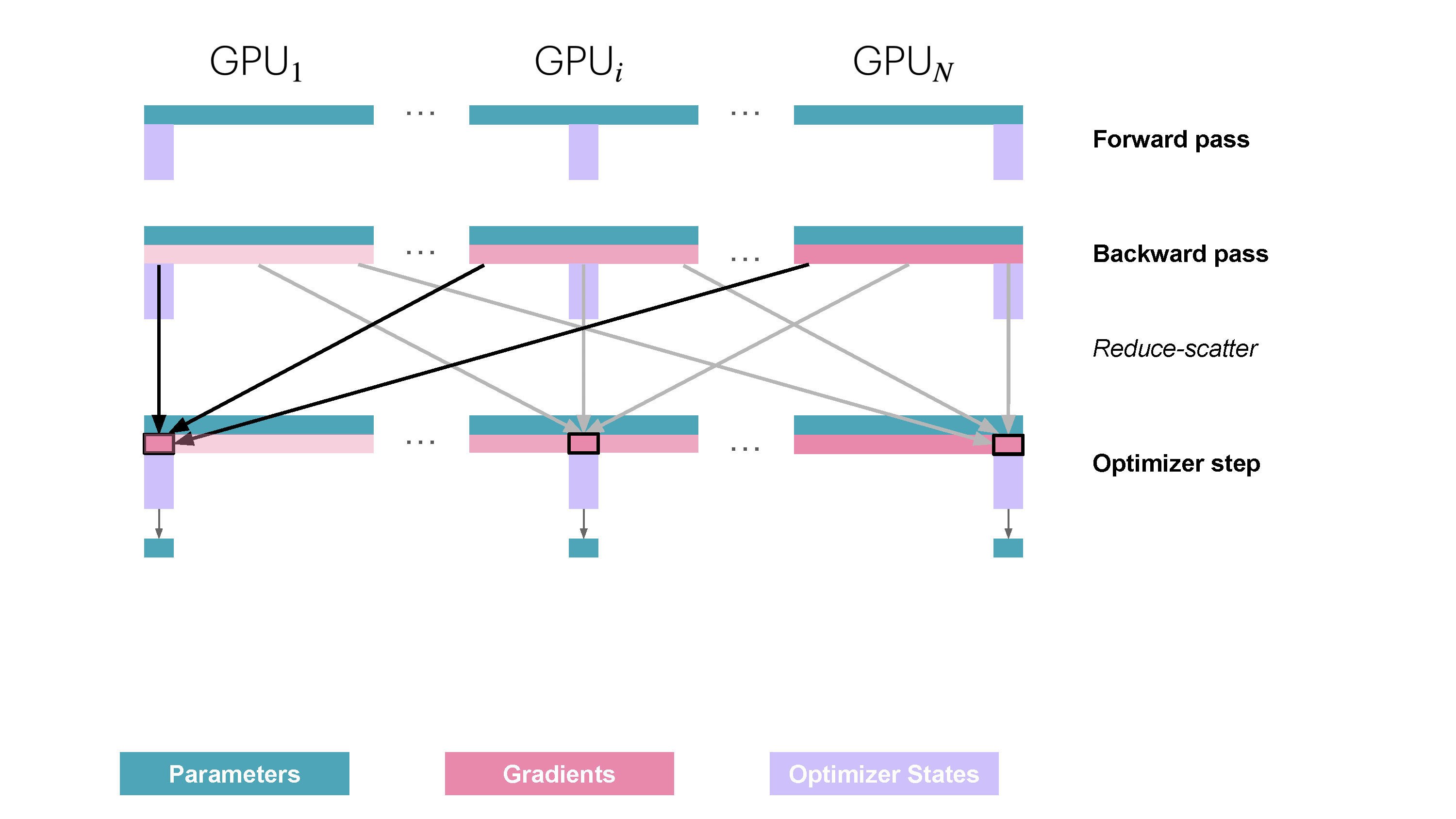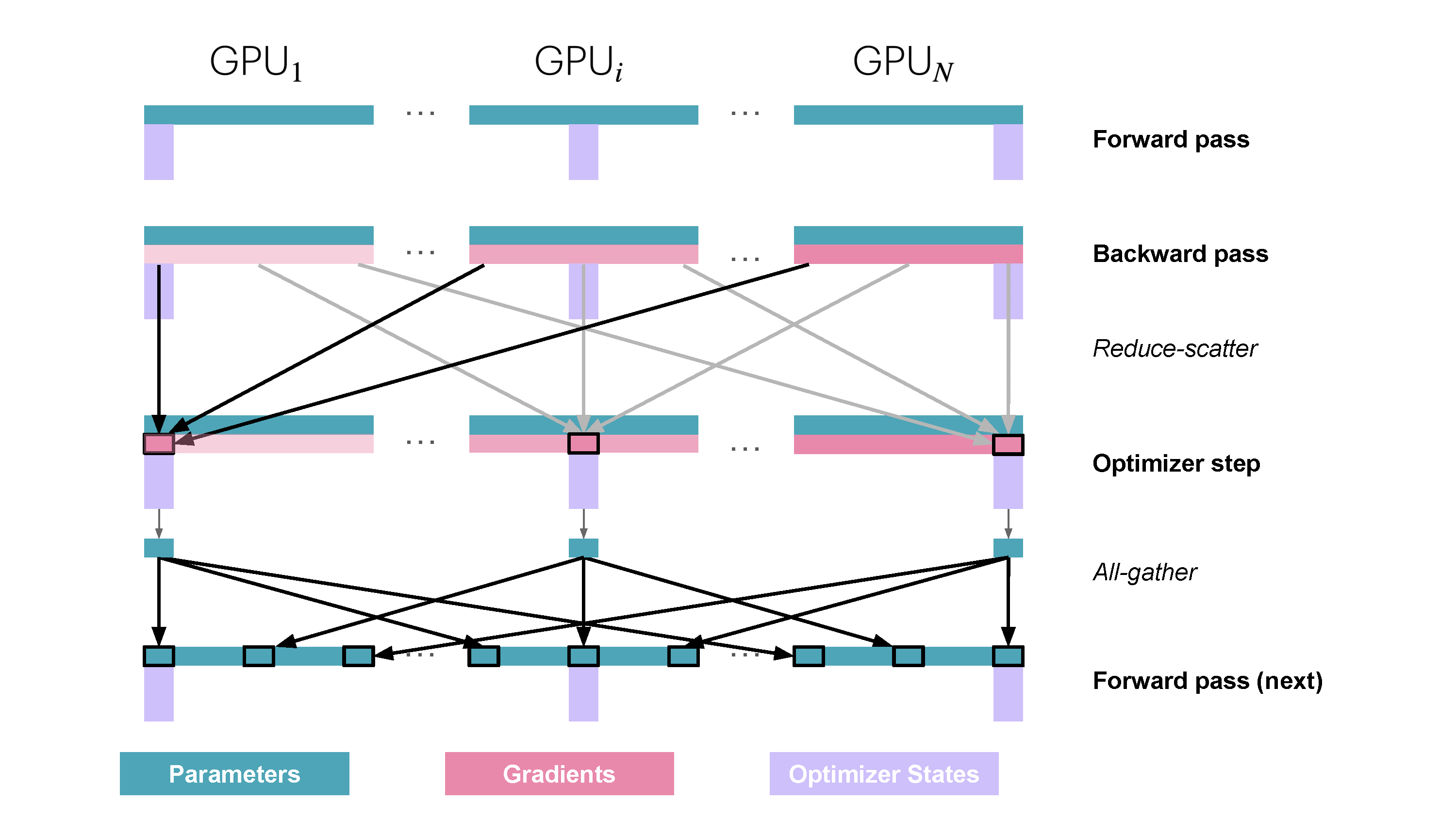
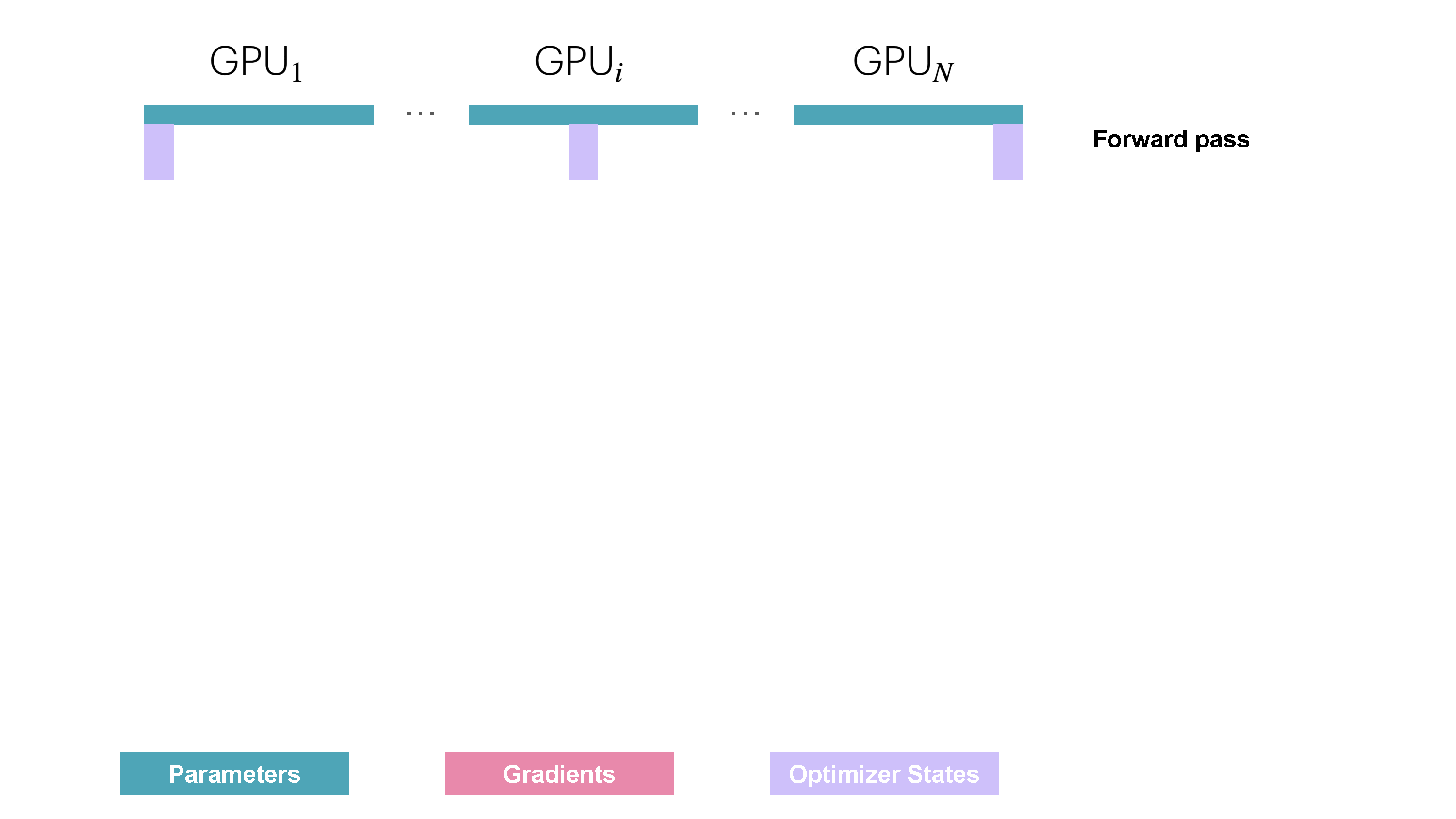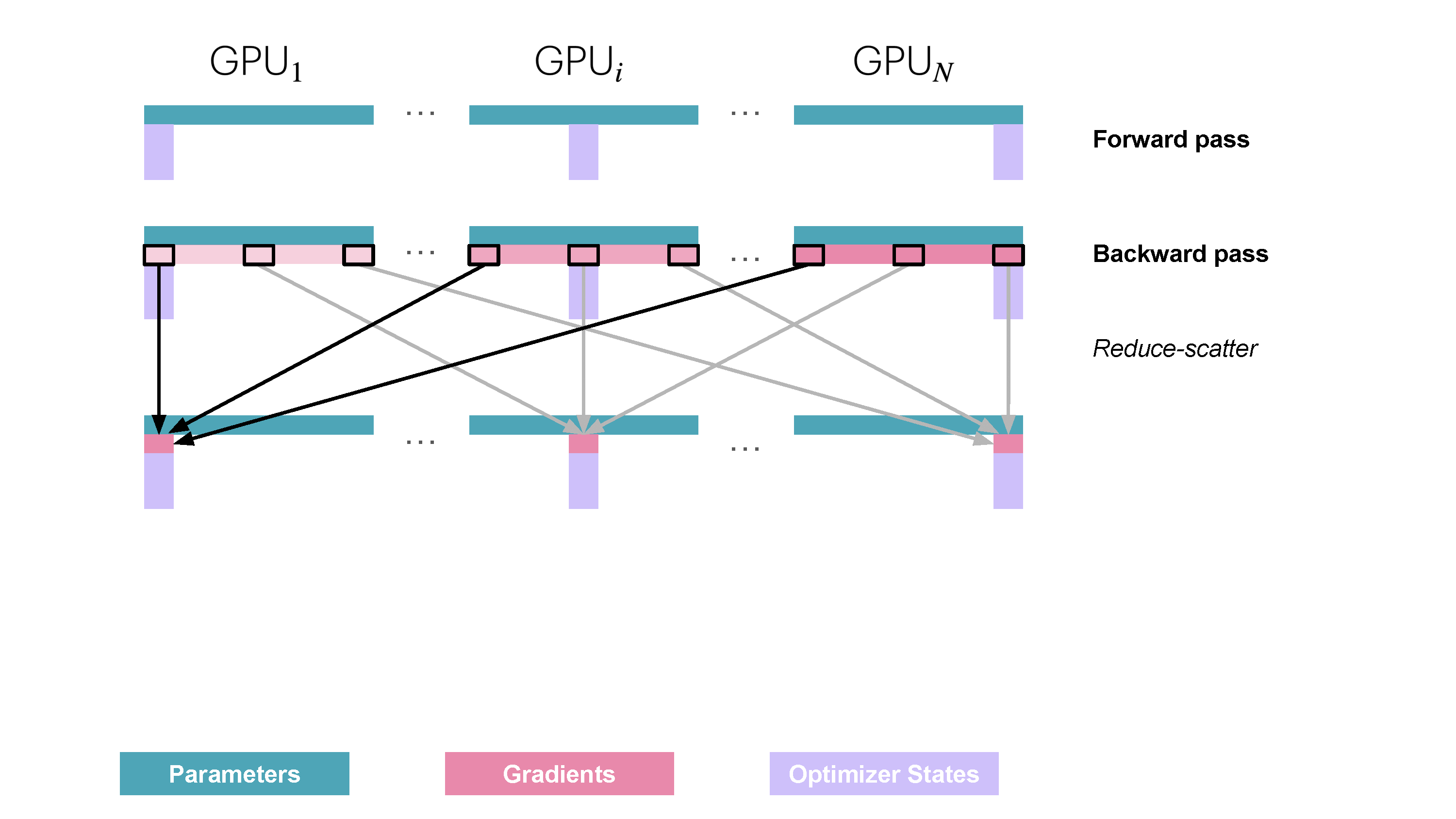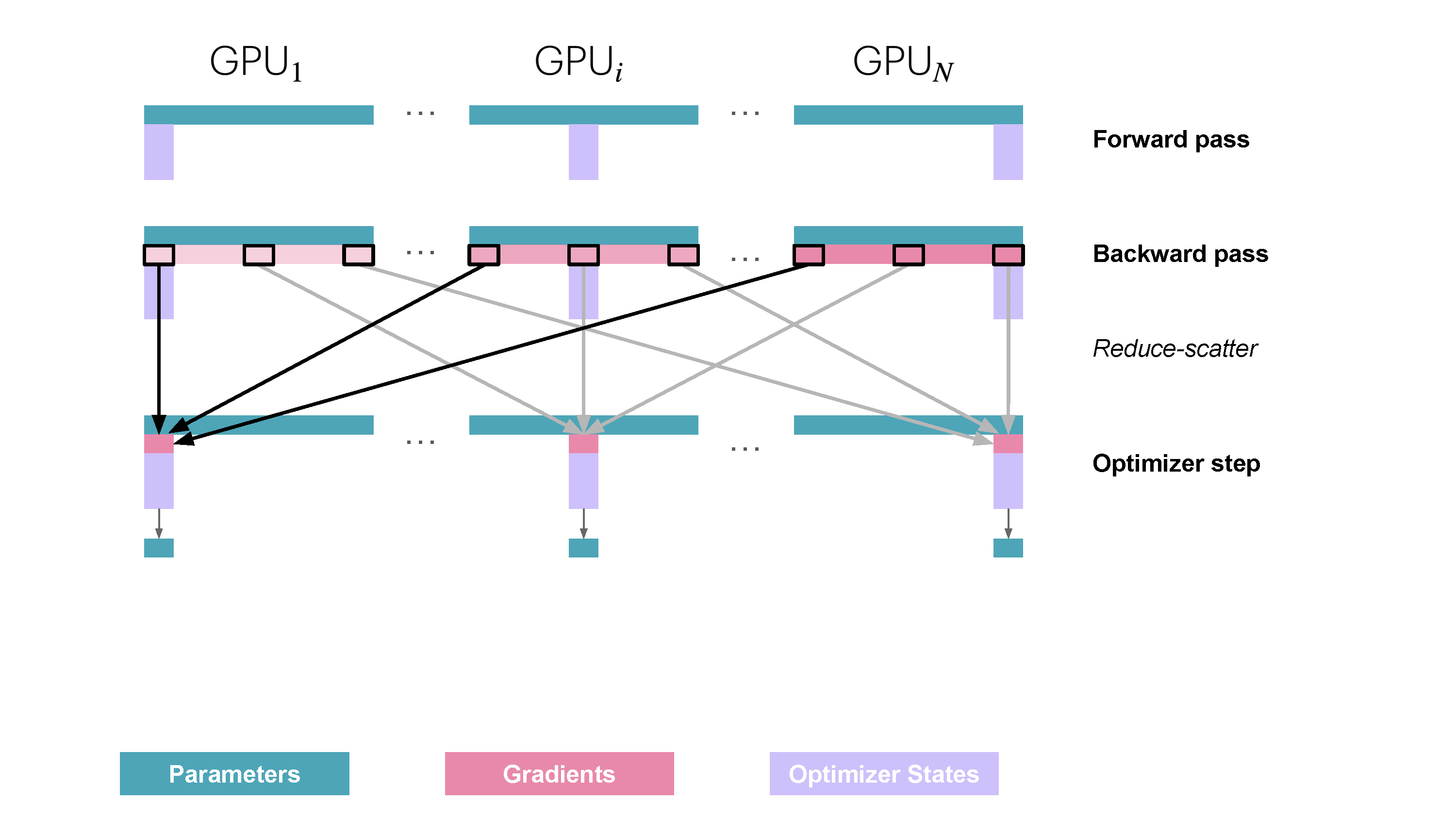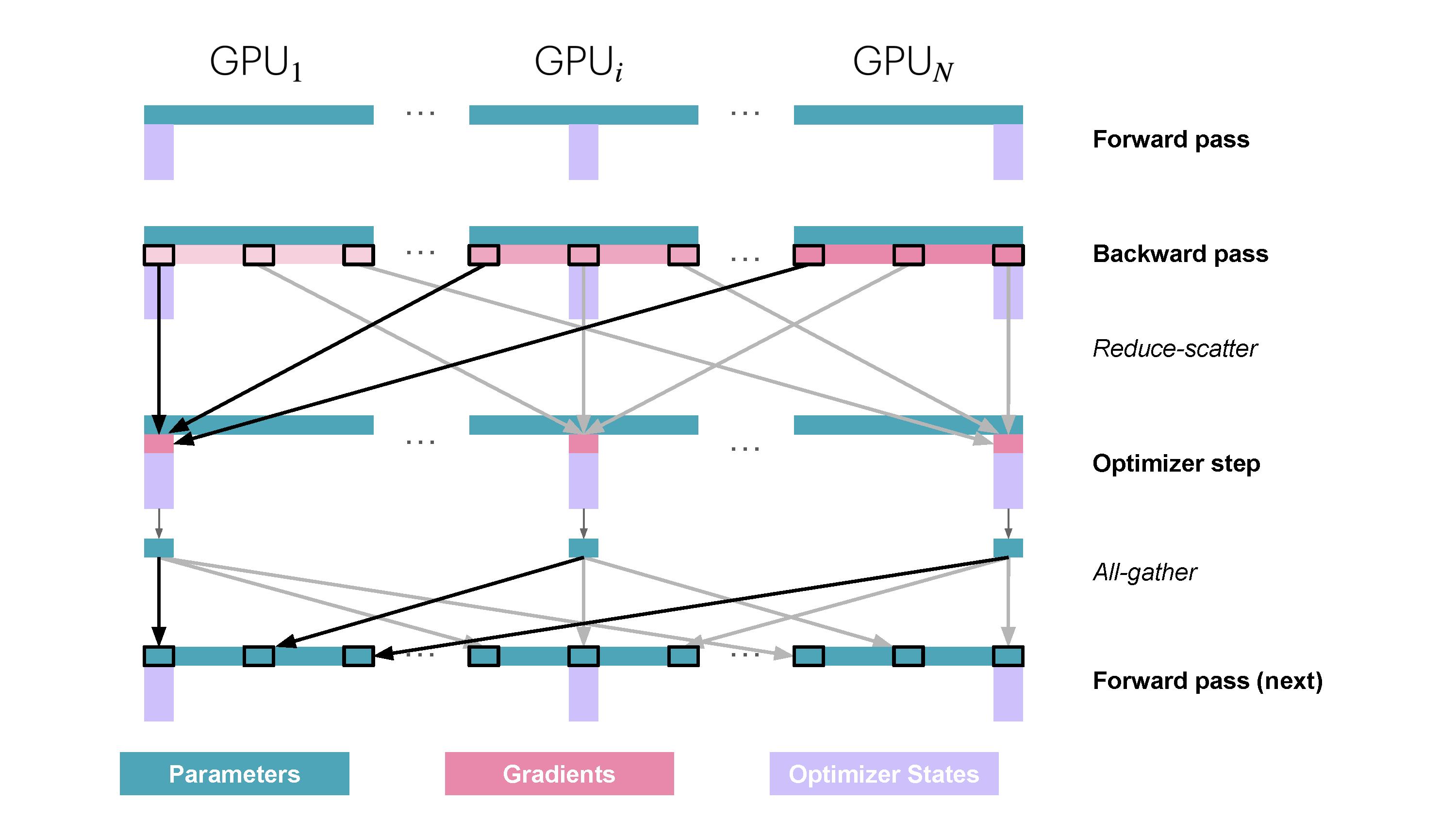
| 641 |
|
| 642 |
-
|
| 643 |
<p>If we don’t accumulate gradients in fp32 this gives us a total memory consumption of <d-math>2\Psi + 2\Psi + 12\Psi</d-math>, and if we accumulate it would be <d-math>2\Psi + 6\Psi + 12\Psi</d-math>. Let’s focus for now on the case without fp32 gradient accumulation for simplicity but you can just add the additional bytes to the gradient term which are affected by ZeRO-2 and 3.</p>
|
| 644 |
|
| 645 |
<p>The idea of ZeRO is to shard these objects across the DP ranks, each node only storing a slice of the items which are reconstructed when and if needed, thereby dividing memory usage by the data parallel degree <d-math>N_d</d-math>:</p>
|
|
@@ -683,7 +712,12 @@
|
|
| 683 |
<li>During forward: We can overlap the all-gather of each layer’s parameters with the forward pass.</li>
|
| 684 |
</ul>
|
| 685 |
|
| 686 |
-
<
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 687 |
|
| 688 |
<p>In ZeRO-1 the optimizer states have been partitioned, which means that each replica only updates <d-math>\frac{1}{N_d}</d-math> of the optimizer states. The keen reader must have noticed that there is no real need to have all gradients on all DP ranks in the first place since only a subset is needed for the optimization step. Meet ZeRO-2!</p>
|
| 689 |
|
|
@@ -709,7 +743,12 @@
|
|
| 709 |
|
| 710 |
<p>For Stage 3 we extend the above approach of sharding optimizer states and gradients over DP replicas up to sharding the model’s parameters.</p>
|
| 711 |
|
| 712 |
-
<
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 713 |
|
| 714 |
<p>So how do we do a forward or backward pass in practice if all parts of the model are distributed? Quite simply we gather them on-demand when we need them. In the forward pass this looks as follows:</p>
|
| 715 |
|
|
@@ -727,7 +766,7 @@
|
|
| 727 |
|
| 728 |
<p>In terms of memory we can see that our equation now reached it’s final form of <d-math>\frac{2\Psi +2\Psi+k\Psi}{N_d}</d-math> which means we can drive memory usage down indefinitely if we can increase the DP rank, at least for the model related parameters. Notice how it doesn’t help with the intermediate activations, for that we can use activation checkpointing and gradient accumulation as we’ve seen in earlier chapters.</p>
|
| 729 |
|
| 730 |
-
<aside>If you want to read more about FSDP1, FSDP2 and some of the implementation complexities around them, you should take some time to go over
|
| 731 |
|
| 732 |
<p><strong>Let’s summarize our journey into DP and ZeRO so far: we have seen that we can increase throughput of training significantly with DP, simply scaling training by adding more model replicas. With ZeRO we can train even models that would ordinarily not fit into a single GPU by sharding the parameters, gradients and optimizers states across DP, while incurring a small communications cost.
|
| 733 |
</strong></p>
|
|
@@ -834,8 +873,12 @@
|
|
| 834 |
|
| 835 |
<p>As we can see, increasing tensor parallelism reduces the memory needed for model parameters, gradients and optimizer states on each GPU. While tensor parallelism does help reduce activation memory in attention and feedforward layers by sharding the matrix multiplications across GPUs, we don't get the full memory benefits we could. This is because operations like layer normalization and dropout still require gathering the full activations on each GPU, partially negating the memory savings. We can do better by finding ways to parallelize these remaining operations as well.</p>
|
| 836 |
|
| 837 |
-
<
|
| 838 |
-
|
|
|
|
|
|
|
|
|
|
|
|
|
| 839 |
|
| 840 |
<p>This raises an interesting question - could we extend tensor parallelism to these remaining operations as well? Indeed, it's possible to parallelize layer norm, dropout and other operations too, which we'll explore next.</p>
|
| 841 |
|
|
@@ -845,7 +888,12 @@
|
|
| 845 |
|
| 846 |
<p>Rather than gathering the full hidden dimension on each GPU (which would defeat the memory benefits of TP), we can instead shard these operations along the sequence length dimension. This approach is called <strong>sequence parallelism (SP)</strong>.</p>
|
| 847 |
|
| 848 |
-
<
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 849 |
|
| 850 |
<p>Sequence parallelism (SP) involves splitting the activations and computations for the parts of the model not handled by tensor parallelism (TP) such as Dropout and LayerNorm, but along the input sequence dimension rather than across hidden dimension. This is needed because these operations require access to the full hidden dimension to compute correctly. For example, LayerNorm needs the full hidden dimension to compute mean and variance:</p>
|
| 851 |
|
|
@@ -1000,7 +1048,12 @@
|
|
| 1000 |
|
| 1001 |
<p>However, there are two limits to TP and SP: 1) if we scale the sequence length the activation memory will still blow up in the TP region and 2) if the model is too big to fit with TP=8 then we will see a massive slow-down due to the inter-node connectivity.</p>
|
| 1002 |
|
| 1003 |
-
<
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1004 |
|
| 1005 |
<p>We can tackle problem 1) with Context parallelism and problem 2) with Pipeline parallelism. Let’s first have a look at Context parallelism!</p>
|
| 1006 |
|
|
@@ -1028,7 +1081,12 @@
|
|
| 1028 |
|
| 1029 |
<p>That sounds very expensive if we do it naively. Is there a way to do this rather efficiently and fast! Thankfully there is: a core technique to handle this communication of key/value pairs efficiently is called <em>Ring Attention</em>.</p>
|
| 1030 |
|
| 1031 |
-
<
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1032 |
|
| 1033 |
<h3>Discovering Ring Attention</h3>
|
| 1034 |
|
|
@@ -1098,11 +1156,11 @@
|
|
| 1098 |
<p>In the TP section we saw that if we try to scale Tensor parallelism past the number of GPUs per single node (typically 4 or 8) we hit a lower bandwidth network called “inter-node connection” which can quite strongly impair our performances. We can see this clearly on e.g. the all-reduce operation when we perform it across several nodes:</p>
|
| 1099 |
|
| 1100 |
<p><img alt="image.png" src="/assets/images/placeholder.png" /></p>
|
| 1101 |
-
<p
|
| 1102 |
|
| 1103 |
<p>Sequence and context parallelism can help for long sequences but don’t help much if sequence length is not the root cause of our memory issues but rather the size of the model itself. For large model (70B+), the size of the weights alone can already push past the limits of the 4-8 GPUs on a single node. We can solve this issue by summoning the fourth (and last) parallelism dimension: “pipeline parallelism”.</p>
|
| 1104 |
|
| 1105 |
-
<p><img alt="image.png" src="/assets/images/placeholder.png" /></p
|
| 1106 |
|
| 1107 |
<p>Pipeline Parallelism is conceptually very simple –we’ll simply spread the layers of our model across GPUs – but the devil lies in implementing it efficiently. Let’s dive in it!</p>
|
| 1108 |
|
|
@@ -1337,8 +1395,15 @@
|
|
| 1337 |
<li>Context Parallelism primarily impacts attention layers since that's where cross-sequence communication is required, with other layers operating independently on sharded sequences.</li>
|
| 1338 |
<li>Expert Parallelism primarly affects the MoE layers (which replace standard MLP blocks), leaving attention and other components unchanged</li>
|
| 1339 |
</ul>
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1340 |
|
| 1341 |
-
<
|
| 1342 |
|
| 1343 |
<table>
|
| 1344 |
<thead>
|
|
@@ -1792,7 +1857,7 @@
|
|
| 1792 |
|
| 1793 |
<p>The meaning of the states can be found in the <a href="https://docs.nvidia.com/nsight-compute/ProfilingGuide/index.html#metrics-reference">Profiling Guide</a>, specifically in the <strong>Warp Stall Reasons</strong> section. There we can read that:</p>
|
| 1794 |
|
| 1795 |
-
<p><em><code>smsp__pcsamp_warps_issue_stalled_mio_throttle</code>: Warp was stalled waiting for the MIO (memory input/output) instruction queue to be not full. This stall reason is high in cases of extreme utilization of the MIO pipelines, which include special math instructions, dynamic branches, as well as shared memory instructions. When caused by shared memory accesses, trying to use fewer but wider loads can reduce pipeline pressure
|
| 1796 |
|
| 1797 |
<p>So it seems warps are stalling waiting for shared memory accesses to return ! To resolve this issue we can apply the <strong>Thread Coarsening</strong> technique by merging several threads into a single coarsened thread, we can significantly reduce shared memory accesses because each coarsened thread can handle multiple output elements which would increase the arithmetic intensity of the kernel.</p>
|
| 1798 |
|
|
|
|
| 222 |
<li>an optimization step using the gradients to update the parameters</li>
|
| 223 |
</ol>
|
| 224 |
|
| 225 |
+
<aside>As we’ll see later, these steps may be repeated or intertwined but for now we’ll start simple.</aside>
|
| 226 |
+
|
| 227 |
<p>It looks generally like this: </p>
|
| 228 |
<p><img alt="image.png" src="assets/images/placeholder.png" /></p>
|
| 229 |
|
|
|
|
|
|
|
| 230 |
<p>In this figure, the boxes on the top line can be seen as successive layers inside a model (same for the last line). The red boxes are the associated gradients for each of these layers, computed during the backward pass.</p>
|
| 231 |
|
| 232 |
<p>The batch size (<d-math>bs</d-math>) is one of the important hyper-parameters for model training and affects both model convergence and throughput.</p>
|
|
|
|
| 241 |
|
| 242 |
<p>In the simplest case, training on a single machine, the <d-math>bs</d-math> (in samples) and <d-math>bst</d-math> can be computed from the model input sequence length (seq) as follows :</p>
|
| 243 |
|
|
|
|
|
|
|
|
|
|
| 244 |
<d-math block>
|
| 245 |
bst=bs *seq
|
| 246 |
</d-math>
|
| 247 |
|
| 248 |
+
<p>From here onward we’ll show the formulas for the batch size in terms of samples but you can always get its token-unit counterpart by multiplying it with the sequence length.</p>
|
| 249 |
+
|
| 250 |
<p>A sweet spot for recent LLM training is typically on the order of 4-60 million tokens per batch. However, a typical issue when scaling the training of our model to these large batch sizes is out-of-memory issues, ie. our GPU doesn’t have enough memory.</p>
|
| 251 |
|
| 252 |
<aside>Note: Llama 1 was trained with a batch size of ~4M tokens for 1.4 trillions tokens while DeepSeek was trained with a batch size of ~60M tokens for 14 trillion tokens.
|
|
|
|
| 266 |
<li>Model gradients</li>
|
| 267 |
<li>Optimizer states</li>
|
| 268 |
</ul>
|
| 269 |
+
|
| 270 |
+
<div class="note-box">
|
| 271 |
+
<p class="note-box-title">📝 Note</p>
|
| 272 |
+
<p class="note-box-content">
|
| 273 |
+
You would think for a model you could compute the memory requirements exactly but there are a few additional memory occupants that makes it hard to be exact:
|
| 274 |
<ul>
|
| 275 |
<li>CUDA Kernels typically require 1-2 GB of GPU memory, which you can quickly verify by running <code>import torch; torch.ones((1, 1)).to("cuda")</code> and then checking the GPU memory with <code>nvidia-smi</code>.</li>
|
| 276 |
<li>Some rest memory usage from buffers, intermediate results and some memory that can’t be used due to fragmentation</li>
|
| 277 |
</ul>
|
| 278 |
+
We’ll neglect these last two contributors as they are typically small and constant factors.
|
| 279 |
+
</p>
|
| 280 |
+
</div>
|
| 281 |
|
| 282 |
<p>These items are stored as tensors which come in different <em>shapes</em> and <em>precisions</em>. The <em>shapes</em> are determined by hyper-parameters such as batch size, sequence length, model hidden dimensions, attention heads, vocabulary size, and potential model sharding as we’ll see later. <em>Precision</em> refers to formats like FP32, BF16, or FP8, which respectively require 4, 2, or 1 byte to store each single value in the tensor.</p>
|
| 283 |
|
|
|
|
| 332 |
\begin{aligned}
|
| 333 |
& m_{params} = 2 * N \\
|
| 334 |
& m_{grad} = 2 * N \\
|
| 335 |
+
& m_{params\_fp32} = 4 * N \\
|
| 336 |
& m_{opt} = (4+4) * N
|
| 337 |
\end{aligned}
|
| 338 |
</d-math>
|
| 339 |
|
| 340 |
+
<div class="note-box">
|
| 341 |
+
<p class="note-box-title">📝 Note</p>
|
| 342 |
+
<p class="note-box-content">
|
| 343 |
+
Some librarie store grads in fp32 which would require an additional <d-math>m_{params\_fp32} = 4 * N</d-math> memory. This is done for example in nanotron, because <code>bf16</code> is lossy for smaller values and we always prioritize stability. See <a href="https://github.com/microsoft/DeepSpeed/issues/1773">this DeepSpeed issue</a> for more information.
|
| 344 |
+
|
| 345 |
+
</p>
|
| 346 |
+
</div>
|
| 347 |
|
| 348 |
<p>Interestingly, mixed precision itself doesn’t save overall memory as it just distributes the memory differently across the three components, and in fact adds another 4 bytes over full precision training if we accumulate gradients in FP32. It’s still advantageous as having the model which does the forward/backward in half precision it allows us to (1) use optimized lower precision operations on the GPU which are faster and (2) reduces the activation memory requirements during the forward pass.</p>
|
| 349 |
|
|
|
|
| 431 |
|
| 432 |
<p><img alt="llama-8b-memory-bars--recomp.png" src="/assets/images/placeholder.png" /></p>
|
| 433 |
|
| 434 |
+
<div class="note-box">
|
| 435 |
+
<p class="note-box-title">📝 Note</p>
|
| 436 |
+
<p class="note-box-content">
|
| 437 |
+
When you’re measuring how efficient your training setup is at using the accelerator’s available compute, you may want to take recomputation into account when measuring the total FLOPS (Floating point operations per second) of your training setup and comparing it to theoretical maximum FLOPS of your GPU/TPU/accelerator to estimate GPU utilization. Taking recomputation into account when calculating FLOPS for a training step gives a value called “hardware FLOPS” which is the real number of operations performed on the accelerator. Dividing this number by the duration of one training step and the maximum accelerator FLOPS yields the <strong><em>Hardware FLOPS Utilization (HFU).</em></strong>
|
| 438 |
+
<br>
|
| 439 |
+
<br>
|
| 440 |
+
However, when comparing various accelerators together, what really matters at the end of the day is the start-to-end time needed to train the same models on the same dataset, ie. if an accelerator allows to skip recomputation and thus perform less operation per second for a faster training it should be rewarded. Thus, alternative is to compute what is called <strong><em>Model FLOPS Utilization (MFU)</em></strong>, which in contrast to HFU only accounts for the required operations to compute the forward+backward passes, and not recomputation, ie. is specific to the model, not the training implementation.
|
| 441 |
+
</p>
|
| 442 |
+
</div>
|
| 443 |
+
|
| 444 |
+
|
| 445 |
+
<aside> </aside>
|
| 446 |
|
| 447 |
+
<aside></aside>
|
| 448 |
|
| 449 |
<p>Most training frameworks these days use FlashAttention (which we’ll cover a bit later) which integrate natively activation recomputation in its optimization strategy by recomputing attention scores and matrices in the backward pass instead of storing them. Thus most people using Flash Attention are already making use of selective recomputation.</p>
|
| 450 |
|
|
|
|
| 476 |
|
| 477 |
<p><img alt="image.png" src="/assets/images/placeholder.png" /></p>
|
| 478 |
|
|
|
|
|
|
|
| 479 |
<aside>Using gradient accumulation means we need to keep buffers where we accumulate gradients which persist throughout a training step. Whereas without gradient accumulation, in the backward gradients are computed while freeing the activations memory, which means a lower peak memory.</aside>
|
| 480 |
|
| 481 |
+
<p><strong>Gradient accumulation allows us to reduce memory of activations which grow linearly with batch size by computing only only partial, micro-batches. There is a small overhead caused by the additional forward and backward passes.</strong></p>
|
| 482 |
+
|
| 483 |
+
|
| 484 |
<p>But if you’ve carefully followed, you probably noticed that the forward/backward passes for each micro-batch can actually be run in parallel. Forward/backward passes are independent from each other, with independent input samples being the only difference. Seems like it’s time to start extending our training to more than one GPU! </p>
|
| 485 |
|
| 486 |
<p>Let’s get a larger workstation 🖥️ with a couple of GPUs and start investigating our first scaling technique called <em><strong>data parallelism</strong> which is just a parallel version of gradient accumulation</em>.</p>
|
|
|
|
| 569 |
|
| 570 |
<p>In PyTorch, this is typically solved by adding a <a href="https://github.com/pytorch/pytorch/blob/5ea67778619c31b13644914deef709199052ee55/torch/nn/parallel/distributed.py#L1408-L1435"><code>model.no_sync()</code></a> decorator, which disables gradient synchronization, on the backward passes which don’t need reduction.</p>
|
| 571 |
|
| 572 |
+
<div class="note-box">
|
| 573 |
+
<p class="note-box-title">📝 Note</p>
|
| 574 |
+
<p class="note-box-content">
|
| 575 |
+
<p>When performing communication operations, tensors must be contiguous in memory. To avoid redundant memory copies during communication, ensure that tensors that will be communicated are stored contiguously in memory. Sometimes we need to allocate additional continuous buffers of the size of activations or model parameters specifically for communication, which contributes to the peak memory usage during training.
|
| 576 |
+
</p>
|
| 577 |
+
</div>
|
| 578 |
+
|
| 579 |
+
<p>Now that we combined both DP and gradient accumulation let's have a look what that means for the global batch size.</p>
|
| 580 |
|
| 581 |
<h3>Revisit global batch size</h3>
|
| 582 |
<p>Let’s update our batch size equation with our newly learned Data Parallelism and Gradient Accumulation parameters:</p>
|
|
|
|
| 603 |
<li>Finally, we determine the number of available GPUs for our target DP. The ratio of GBS to DP gives us the remaining number of gradient accumulation steps needed for the desired GBS. </li>
|
| 604 |
</ol>
|
| 605 |
|
| 606 |
+
<aside>For instance DeepSeek and Llama models are trained with a 4k tokens sequence length during the main pretraining phase.<br><br>The reason 2-8k work well for pretraining is that documents that are longer are very rare on the web. See this <a href="https://www.harmdevries.com/post/context-length/">Harm’s blogpost</a> for a detailed analysis.</aside>
|
| 607 |
|
|
|
|
|
|
|
| 608 |
|
| 609 |
<p>If the gradient accumulation ratio is lower than one, i.e. we have too many GPUs a.k.a GPU-rich 🤑 (!), we can either choose to not use all our GPUs, explore a larger global batch size or test if a lower MBS will speed up training. In the latter case we’ll end up prioritizing throughput over individual GPU compute efficiency, using a smaller MBS than possible in order to speed up training.</p>
|
| 610 |
|
| 611 |
<p>Time to take a concrete example: Let’s say we want to train a recent model with a GBS of 4M tokens and a sequence length of 4k. This means our batch size will be 1024 samples (we pick powers of two). We observe that a single GPU can only fit MBS=2 in memory and we have 128 GPUs available for training. This means with 4 gradient accumulation steps we’ll achieve our goal of 1024 samples or 4M tokens per training step. Now what if we suddenly have 512 GPUs available? We can achieve the same GBS and thus identical training by keeping MBS=2 and setting gradient accumulation steps to 1 and achieve faster training!</p>
|
| 612 |
|
| 613 |
+
<div class="note-box">
|
| 614 |
+
<p class="note-box-title">📝 Note</p>
|
| 615 |
+
<p class="note-box-content">
|
| 616 |
+
<p>Bear in mind that at the 512+ GPUs scale, depending on the network used, the communication operations will start to be bound by <em>ring latency</em> (time required for a signal to propagate once around the ring) which means we can no longer fully overlap the DP communications. This will decrease our compute efficiency and hit our throughput. In this case we should start exploring other dimensions to parallelize on.
|
| 617 |
+
</p>
|
| 618 |
+
</div>
|
| 619 |
|
| 620 |
<p>While data parallelism cleverly overlaps the all-reduce gradient synchronization with backward computation to save time, this benefit starts to break down at large scales. As we add more and more GPUs (hundreds or thousands), the overhead of coordinating between them grows significantly. The end result? We get less and less efficient returns from each additional GPU we add to the system:</p>
|
| 621 |
|
|
|
|
| 640 |
|
| 641 |
<p>In this section we will introduce DeepSpeed ZeRO (<strong>Ze</strong>ro <strong>R</strong>edundancy <strong>O</strong>ptimizer), a memory optimization technology designed to reduce memory redundancies in LLM training.</p>
|
| 642 |
|
|
|
|
|
|
|
| 643 |
<p>While Data Parallelism is very efficient in scaling training, the naive replication of optimizer states, gradients, and parameters across each DP rank introduces a significant memory redundancy. ZeRO eliminates memory redundancy by partitioning the optimizer states, gradients, and parameters across the data parallel dimension, while still allowing computation with the full set of parameters. This sometimes requires more communications between DP ranks which may or may not be fully overlapped as we’ll see next!</p>
|
| 644 |
|
| 645 |
+
<aside>We’ll focus on ZeRO-1 to ZeRO-3 in this blog as it should give a broad view on how it helps reduce memory while showing the tradeoffs to take into account. You can find more ZeRO flavors in the <a href="https://www.deepspeed.ai/tutorials/zero/">DeepSpeed docs</a>.</aside>
|
| 646 |
+
|
| 647 |
<p>This approach is organized into three possible optimization stage of ZeRO:</p>
|
| 648 |
|
| 649 |
<ul>
|
|
|
|
| 652 |
<li>ZeRO-3 (also called FSDP for “Fully-Sharded Data Parallelism”): optimizer state + gradient + parameter partitioning</li>
|
| 653 |
</ul>
|
| 654 |
|
|
|
|
|
|
|
| 655 |
<aside>When we say partitioning, it means alongside the DP axis, as ZeRO is part of Data Parallelism. We’ll see later that we can partition alongside other axes.</aside>
|
| 656 |
|
| 657 |
+
<p>You might be missing the activations among the things we can shard. Since each DP replica of the model receives a different micro-batch the activations on each DP rank also differ so they are not duplicated and thus can’t be sharded!</p>
|
| 658 |
+
|
| 659 |
<p>Let’s have a closer look how much we can save with the partitioning of each ZeRO stage!</p>
|
| 660 |
|
| 661 |
<h4>Memory usage revisited</h4>
|
|
|
|
| 669 |
<li>- Model’s gradients in fp32: <d-math>4\Psi</d-math> (optional, only accounted if we want to accumulate grads in fp32)</li>
|
| 670 |
</ul>
|
| 671 |
|
|
|
|
| 672 |
<p>If we don’t accumulate gradients in fp32 this gives us a total memory consumption of <d-math>2\Psi + 2\Psi + 12\Psi</d-math>, and if we accumulate it would be <d-math>2\Psi + 6\Psi + 12\Psi</d-math>. Let’s focus for now on the case without fp32 gradient accumulation for simplicity but you can just add the additional bytes to the gradient term which are affected by ZeRO-2 and 3.</p>
|
| 673 |
|
| 674 |
<p>The idea of ZeRO is to shard these objects across the DP ranks, each node only storing a slice of the items which are reconstructed when and if needed, thereby dividing memory usage by the data parallel degree <d-math>N_d</d-math>:</p>
|
|
|
|
| 712 |
<li>During forward: We can overlap the all-gather of each layer’s parameters with the forward pass.</li>
|
| 713 |
</ul>
|
| 714 |
|
| 715 |
+
<div class="note-box">
|
| 716 |
+
<p class="note-box-title">📝 Note</p>
|
| 717 |
+
<p class="note-box-content">
|
| 718 |
+
<p>Unfortunately these techniques are not straightforward to implement and require sophisticated use of hooks/bucketing. In practice we can just use ZeRO-3/FSDP implementation where the FSDPUnit is the entire model, more details about this later.
|
| 719 |
+
</p>
|
| 720 |
+
</div>
|
| 721 |
|
| 722 |
<p>In ZeRO-1 the optimizer states have been partitioned, which means that each replica only updates <d-math>\frac{1}{N_d}</d-math> of the optimizer states. The keen reader must have noticed that there is no real need to have all gradients on all DP ranks in the first place since only a subset is needed for the optimization step. Meet ZeRO-2!</p>
|
| 723 |
|
|
|
|
| 743 |
|
| 744 |
<p>For Stage 3 we extend the above approach of sharding optimizer states and gradients over DP replicas up to sharding the model’s parameters.</p>
|
| 745 |
|
| 746 |
+
<div class="note-box">
|
| 747 |
+
<p class="note-box-title">📝 Note</p>
|
| 748 |
+
<p class="note-box-content">
|
| 749 |
+
<p>This stage is also called FSDP (Fully Shared Data Parallelism) in PyTorch native implementation. We’ll just refer to ZeRO-3 in this blogpost but you can think of FSDP wherever you see it.
|
| 750 |
+
</p>
|
| 751 |
+
</div>
|
| 752 |
|
| 753 |
<p>So how do we do a forward or backward pass in practice if all parts of the model are distributed? Quite simply we gather them on-demand when we need them. In the forward pass this looks as follows:</p>
|
| 754 |
|
|
|
|
| 766 |
|
| 767 |
<p>In terms of memory we can see that our equation now reached it’s final form of <d-math>\frac{2\Psi +2\Psi+k\Psi}{N_d}</d-math> which means we can drive memory usage down indefinitely if we can increase the DP rank, at least for the model related parameters. Notice how it doesn’t help with the intermediate activations, for that we can use activation checkpointing and gradient accumulation as we’ve seen in earlier chapters.</p>
|
| 768 |
|
| 769 |
+
<aside>If you want to read more about FSDP1, FSDP2 and some of the implementation complexities around them, you should take some time to go over <a href="https://christianjmills.com/posts/mastering-llms-course-notes/conference-talk-012/">this nice blog</a>.</aside>
|
| 770 |
|
| 771 |
<p><strong>Let’s summarize our journey into DP and ZeRO so far: we have seen that we can increase throughput of training significantly with DP, simply scaling training by adding more model replicas. With ZeRO we can train even models that would ordinarily not fit into a single GPU by sharding the parameters, gradients and optimizers states across DP, while incurring a small communications cost.
|
| 772 |
</strong></p>
|
|
|
|
| 873 |
|
| 874 |
<p>As we can see, increasing tensor parallelism reduces the memory needed for model parameters, gradients and optimizer states on each GPU. While tensor parallelism does help reduce activation memory in attention and feedforward layers by sharding the matrix multiplications across GPUs, we don't get the full memory benefits we could. This is because operations like layer normalization and dropout still require gathering the full activations on each GPU, partially negating the memory savings. We can do better by finding ways to parallelize these remaining operations as well.</p>
|
| 875 |
|
| 876 |
+
<div class="note-box">
|
| 877 |
+
<p class="note-box-title">📝 Note</p>
|
| 878 |
+
<p class="note-box-content">
|
| 879 |
+
<p>One interesting note about layer normalization in tensor parallel training - since each TP rank sees the same activations after the all-gather, the layer norm weights don't actually need an all-reduce to sync their gradients after the backward pass. They naturally stay in sync across ranks. However, for dropout operations, we must make sure to sync the random seed across TP ranks to maintain deterministic behavior.
|
| 880 |
+
</p>
|
| 881 |
+
</div>
|
| 882 |
|
| 883 |
<p>This raises an interesting question - could we extend tensor parallelism to these remaining operations as well? Indeed, it's possible to parallelize layer norm, dropout and other operations too, which we'll explore next.</p>
|
| 884 |
|
|
|
|
| 888 |
|
| 889 |
<p>Rather than gathering the full hidden dimension on each GPU (which would defeat the memory benefits of TP), we can instead shard these operations along the sequence length dimension. This approach is called <strong>sequence parallelism (SP)</strong>.</p>
|
| 890 |
|
| 891 |
+
<div class="note-box">
|
| 892 |
+
<p class="note-box-title">📝 Note</p>
|
| 893 |
+
<p class="note-box-content">
|
| 894 |
+
<p>The term Sequence Parallelism is a bit overloaded: the Sequence Parallelism in this section is tightly coupled to Tensor Parallelism and applies to dropout and layer norm operation. However, when we will move to longer sequences the attention computation will become a bottleneck, which calls for techniques such as Ring-Attention, which are sometimes also called <em>Sequence Parallelism</em> but we’ll refer to them as <em>Context Parallelism</em> to differentiate the two approaches. So each time you see sequence parallelism, remember that it is used together with tensor parallelism (in contrast to context parallelism, which can be used independently).
|
| 895 |
+
</p>
|
| 896 |
+
</div>
|
| 897 |
|
| 898 |
<p>Sequence parallelism (SP) involves splitting the activations and computations for the parts of the model not handled by tensor parallelism (TP) such as Dropout and LayerNorm, but along the input sequence dimension rather than across hidden dimension. This is needed because these operations require access to the full hidden dimension to compute correctly. For example, LayerNorm needs the full hidden dimension to compute mean and variance:</p>
|
| 899 |
|
|
|
|
| 1048 |
|
| 1049 |
<p>However, there are two limits to TP and SP: 1) if we scale the sequence length the activation memory will still blow up in the TP region and 2) if the model is too big to fit with TP=8 then we will see a massive slow-down due to the inter-node connectivity.</p>
|
| 1050 |
|
| 1051 |
+
<div class="note-box">
|
| 1052 |
+
<p class="note-box-title">📝 Note</p>
|
| 1053 |
+
<p class="note-box-content">
|
| 1054 |
+
<p>Since LayerNorms in the SP region operate on different portions of the sequence, their gradients will differ across TP ranks. To ensure the weights stay synchronized, we need to allreduce their gradients during the backward pass, similar to how DP ensures weights stay in sync. This is a small communication overhead since LayerNorm has relatively few parameters.
|
| 1055 |
+
</p>
|
| 1056 |
+
</div>
|
| 1057 |
|
| 1058 |
<p>We can tackle problem 1) with Context parallelism and problem 2) with Pipeline parallelism. Let’s first have a look at Context parallelism!</p>
|
| 1059 |
|
|
|
|
| 1081 |
|
| 1082 |
<p>That sounds very expensive if we do it naively. Is there a way to do this rather efficiently and fast! Thankfully there is: a core technique to handle this communication of key/value pairs efficiently is called <em>Ring Attention</em>.</p>
|
| 1083 |
|
| 1084 |
+
<div class="note-box">
|
| 1085 |
+
<p class="note-box-title">📝 Note</p>
|
| 1086 |
+
<p class="note-box-content">
|
| 1087 |
+
<p>Context Parallelism shares some conceptual similarities with Flash Attention (see later for more details) - both techniques rely on online softmax computation to reduce memory usage. While Flash Attention focuses on optimizing the attention computation itself on a single GPU, Context Parallelism achieves memory reduction by distributing the sequence across multiple GPUs.
|
| 1088 |
+
</p>
|
| 1089 |
+
</div>
|
| 1090 |
|
| 1091 |
<h3>Discovering Ring Attention</h3>
|
| 1092 |
|
|
|
|
| 1156 |
<p>In the TP section we saw that if we try to scale Tensor parallelism past the number of GPUs per single node (typically 4 or 8) we hit a lower bandwidth network called “inter-node connection” which can quite strongly impair our performances. We can see this clearly on e.g. the all-reduce operation when we perform it across several nodes:</p>
|
| 1157 |
|
| 1158 |
<p><img alt="image.png" src="/assets/images/placeholder.png" /></p>
|
| 1159 |
+
<p>Inter-node communication bandwidth measurements across different node counts, showing median (lines) and 5th-95th percentile ranges (shaded areas) for AllReduce, AllGather and ReduceScatter operations.</p>
|
| 1160 |
|
| 1161 |
<p>Sequence and context parallelism can help for long sequences but don’t help much if sequence length is not the root cause of our memory issues but rather the size of the model itself. For large model (70B+), the size of the weights alone can already push past the limits of the 4-8 GPUs on a single node. We can solve this issue by summoning the fourth (and last) parallelism dimension: “pipeline parallelism”.</p>
|
| 1162 |
|
| 1163 |
+
<p><img alt="image.png" src="/assets/images/placeholder.png" /></p>
|
| 1164 |
|
| 1165 |
<p>Pipeline Parallelism is conceptually very simple –we’ll simply spread the layers of our model across GPUs – but the devil lies in implementing it efficiently. Let’s dive in it!</p>
|
| 1166 |
|
|
|
|
| 1395 |
<li>Context Parallelism primarily impacts attention layers since that's where cross-sequence communication is required, with other layers operating independently on sharded sequences.</li>
|
| 1396 |
<li>Expert Parallelism primarly affects the MoE layers (which replace standard MLP blocks), leaving attention and other components unchanged</li>
|
| 1397 |
</ul>
|
| 1398 |
+
|
| 1399 |
+
<div class="note-box">
|
| 1400 |
+
<p class="note-box-title">📝 Note</p>
|
| 1401 |
+
<p class="note-box-content">
|
| 1402 |
+
<p>This similarity between EP and DP in terms of input handling is why some implementations consider Expert Parallelism to be a subgroup of Data Parallelism, with the key difference being that EP uses specialized expert routing rather than having all GPUs process inputs through identical model copies.
|
| 1403 |
+
</p>
|
| 1404 |
+
</div>
|
| 1405 |
|
| 1406 |
+
<p>TODO: the text between the table and figueres is still a bit sparse.</p>
|
| 1407 |
|
| 1408 |
<table>
|
| 1409 |
<thead>
|
|
|
|
| 1857 |
|
| 1858 |
<p>The meaning of the states can be found in the <a href="https://docs.nvidia.com/nsight-compute/ProfilingGuide/index.html#metrics-reference">Profiling Guide</a>, specifically in the <strong>Warp Stall Reasons</strong> section. There we can read that:</p>
|
| 1859 |
|
| 1860 |
+
<p><em><code>"smsp__pcsamp_warps_issue_stalled_mio_throttle</code>: Warp was stalled waiting for the MIO (memory input/output) instruction queue to be not full. This stall reason is high in cases of extreme utilization of the MIO pipelines, which include special math instructions, dynamic branches, as well as shared memory instructions. When caused by shared memory accesses, trying to use fewer but wider loads can reduce pipeline pressure."</em></p>
|
| 1861 |
|
| 1862 |
<p>So it seems warps are stalling waiting for shared memory accesses to return ! To resolve this issue we can apply the <strong>Thread Coarsening</strong> technique by merging several threads into a single coarsened thread, we can significantly reduce shared memory accesses because each coarsened thread can handle multiple output elements which would increase the arithmetic intensity of the kernel.</p>
|
| 1863 |
|
dist/style.css
CHANGED
|
@@ -334,4 +334,39 @@ d-contents nav > ul > li > a:hover {
|
|
| 334 |
#graph svg rect {
|
| 335 |
cursor: pointer;
|
| 336 |
}
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 337 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 334 |
#graph svg rect {
|
| 335 |
cursor: pointer;
|
| 336 |
}
|
| 337 |
+
.note-box {
|
| 338 |
+
background-color: #f6f8fa;
|
| 339 |
+
border-left: 4px solid #444444;
|
| 340 |
+
padding: 1rem;
|
| 341 |
+
margin: 1rem 0; /* Keep this modest margin */
|
| 342 |
+
border-radius: 6px;
|
| 343 |
+
/* Add this to ensure the box only takes up needed space */
|
| 344 |
+
display: inline-block;
|
| 345 |
+
width: 100%;
|
| 346 |
+
}
|
| 347 |
+
|
| 348 |
+
.note-box-title {
|
| 349 |
+
margin: 0;
|
| 350 |
+
color: #444444;
|
| 351 |
+
font-weight: 600;
|
| 352 |
+
}
|
| 353 |
|
| 354 |
+
.note-box-content {
|
| 355 |
+
margin-top: 0.5rem;
|
| 356 |
+
margin-bottom: 0; /* Ensure no bottom margin */
|
| 357 |
+
color: #24292f;
|
| 358 |
+
}
|
| 359 |
+
|
| 360 |
+
/* For dark mode support */
|
| 361 |
+
@media (prefers-color-scheme: dark) {
|
| 362 |
+
.note-box {
|
| 363 |
+
background-color: #1c1c1c;
|
| 364 |
+
border-left-color: #888888;
|
| 365 |
+
}
|
| 366 |
+
.note-box-title {
|
| 367 |
+
color: #888888;
|
| 368 |
+
}
|
| 369 |
+
.note-box-content {
|
| 370 |
+
color: #d4d4d4;
|
| 371 |
+
}
|
| 372 |
+
}
|
src/index.html
CHANGED
|
@@ -222,11 +222,11 @@
|
|
| 222 |
<li>an optimization step using the gradients to update the parameters</li>
|
| 223 |
</ol>
|
| 224 |
|
|
|
|
|
|
|
| 225 |
<p>It looks generally like this: </p>
|
| 226 |
<p><img alt="image.png" src="assets/images/placeholder.png" /></p>
|
| 227 |
|
| 228 |
-
<aside>As we’ll see later, these steps may be repeated or intertwined but for now we’ll start simple.</aside>
|
| 229 |
-
|
| 230 |
<p>In this figure, the boxes on the top line can be seen as successive layers inside a model (same for the last line). The red boxes are the associated gradients for each of these layers, computed during the backward pass.</p>
|
| 231 |
|
| 232 |
<p>The batch size (<d-math>bs</d-math>) is one of the important hyper-parameters for model training and affects both model convergence and throughput.</p>
|
|
@@ -241,13 +241,12 @@
|
|
| 241 |
|
| 242 |
<p>In the simplest case, training on a single machine, the <d-math>bs</d-math> (in samples) and <d-math>bst</d-math> can be computed from the model input sequence length (seq) as follows :</p>
|
| 243 |
|
| 244 |
-
<aside><p>From here onward we’ll show the formulas for the batch size in terms of samples but you can always get its token-unit counterpart by multiplying it with the sequence length.
|
| 245 |
-
</aside>
|
| 246 |
-
|
| 247 |
<d-math block>
|
| 248 |
bst=bs *seq
|
| 249 |
</d-math>
|
| 250 |
|
|
|
|
|
|
|
| 251 |
<p>A sweet spot for recent LLM training is typically on the order of 4-60 million tokens per batch. However, a typical issue when scaling the training of our model to these large batch sizes is out-of-memory issues, ie. our GPU doesn’t have enough memory.</p>
|
| 252 |
|
| 253 |
<aside>Note: Llama 1 was trained with a batch size of ~4M tokens for 1.4 trillions tokens while DeepSeek was trained with a batch size of ~60M tokens for 14 trillion tokens.
|
|
@@ -267,13 +266,18 @@
|
|
| 267 |
<li>Model gradients</li>
|
| 268 |
<li>Optimizer states</li>
|
| 269 |
</ul>
|
| 270 |
-
|
| 271 |
-
<
|
|
|
|
|
|
|
|
|
|
| 272 |
<ul>
|
| 273 |
<li>CUDA Kernels typically require 1-2 GB of GPU memory, which you can quickly verify by running <code>import torch; torch.ones((1, 1)).to("cuda")</code> and then checking the GPU memory with <code>nvidia-smi</code>.</li>
|
| 274 |
<li>Some rest memory usage from buffers, intermediate results and some memory that can’t be used due to fragmentation</li>
|
| 275 |
</ul>
|
| 276 |
-
We’ll neglect these last two contributors as they are typically small and constant factors
|
|
|
|
|
|
|
| 277 |
|
| 278 |
<p>These items are stored as tensors which come in different <em>shapes</em> and <em>precisions</em>. The <em>shapes</em> are determined by hyper-parameters such as batch size, sequence length, model hidden dimensions, attention heads, vocabulary size, and potential model sharding as we’ll see later. <em>Precision</em> refers to formats like FP32, BF16, or FP8, which respectively require 4, 2, or 1 byte to store each single value in the tensor.</p>
|
| 279 |
|
|
@@ -328,13 +332,18 @@
|
|
| 328 |
\begin{aligned}
|
| 329 |
& m_{params} = 2 * N \\
|
| 330 |
& m_{grad} = 2 * N \\
|
| 331 |
-
& m_{
|
| 332 |
& m_{opt} = (4+4) * N
|
| 333 |
\end{aligned}
|
| 334 |
</d-math>
|
| 335 |
|
| 336 |
-
<
|
| 337 |
-
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 338 |
|
| 339 |
<p>Interestingly, mixed precision itself doesn’t save overall memory as it just distributes the memory differently across the three components, and in fact adds another 4 bytes over full precision training if we accumulate gradients in FP32. It’s still advantageous as having the model which does the forward/backward in half precision it allows us to (1) use optimized lower precision operations on the GPU which are faster and (2) reduces the activation memory requirements during the forward pass.</p>
|
| 340 |
|
|
@@ -422,9 +431,20 @@
|
|
| 422 |
|
| 423 |
<p><img alt="llama-8b-memory-bars--recomp.png" src="/assets/images/placeholder.png" /></p>
|
| 424 |
|
| 425 |
-
<
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 426 |
|
| 427 |
-
<aside
|
| 428 |
|
| 429 |
<p>Most training frameworks these days use FlashAttention (which we’ll cover a bit later) which integrate natively activation recomputation in its optimization strategy by recomputing attention scores and matrices in the backward pass instead of storing them. Thus most people using Flash Attention are already making use of selective recomputation.</p>
|
| 430 |
|
|
@@ -456,10 +476,11 @@
|
|
| 456 |
|
| 457 |
<p><img alt="image.png" src="/assets/images/placeholder.png" /></p>
|
| 458 |
|
| 459 |
-
<p><strong>Gradient accumulation allows us to reduce memory of activations which grow linearly with batch size by computing only only partial, micro-batches. There is a small overhead caused by the additional forward and backward passes.</strong></p>
|
| 460 |
-
|
| 461 |
<aside>Using gradient accumulation means we need to keep buffers where we accumulate gradients which persist throughout a training step. Whereas without gradient accumulation, in the backward gradients are computed while freeing the activations memory, which means a lower peak memory.</aside>
|
| 462 |
|
|
|
|
|
|
|
|
|
|
| 463 |
<p>But if you’ve carefully followed, you probably noticed that the forward/backward passes for each micro-batch can actually be run in parallel. Forward/backward passes are independent from each other, with independent input samples being the only difference. Seems like it’s time to start extending our training to more than one GPU! </p>
|
| 464 |
|
| 465 |
<p>Let’s get a larger workstation 🖥️ with a couple of GPUs and start investigating our first scaling technique called <em><strong>data parallelism</strong> which is just a parallel version of gradient accumulation</em>.</p>
|
|
@@ -548,7 +569,14 @@
|
|
| 548 |
|
| 549 |
<p>In PyTorch, this is typically solved by adding a <a href="https://github.com/pytorch/pytorch/blob/5ea67778619c31b13644914deef709199052ee55/torch/nn/parallel/distributed.py#L1408-L1435"><code>model.no_sync()</code></a> decorator, which disables gradient synchronization, on the backward passes which don’t need reduction.</p>
|
| 550 |
|
| 551 |
-
<
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 552 |
|
| 553 |
<h3>Revisit global batch size</h3>
|
| 554 |
<p>Let’s update our batch size equation with our newly learned Data Parallelism and Gradient Accumulation parameters:</p>
|
|
@@ -575,17 +603,19 @@
|
|
| 575 |
<li>Finally, we determine the number of available GPUs for our target DP. The ratio of GBS to DP gives us the remaining number of gradient accumulation steps needed for the desired GBS. </li>
|
| 576 |
</ol>
|
| 577 |
|
| 578 |
-
<aside>For instance DeepSeek and Llama models are trained with a 4k tokens sequence length during the main pretraining phase.</aside>
|
| 579 |
|
| 580 |
-
<aside>The reason 2-8k work well for pretraining is that documents that are longer are very rare on the web. See this <a href="https://www.harmdevries.com/post/context-length/">Harm’s blogpost</a> for a detailed analysis.
|
| 581 |
-
</aside>
|
| 582 |
|
| 583 |
<p>If the gradient accumulation ratio is lower than one, i.e. we have too many GPUs a.k.a GPU-rich 🤑 (!), we can either choose to not use all our GPUs, explore a larger global batch size or test if a lower MBS will speed up training. In the latter case we’ll end up prioritizing throughput over individual GPU compute efficiency, using a smaller MBS than possible in order to speed up training.</p>
|
| 584 |
|
| 585 |
<p>Time to take a concrete example: Let’s say we want to train a recent model with a GBS of 4M tokens and a sequence length of 4k. This means our batch size will be 1024 samples (we pick powers of two). We observe that a single GPU can only fit MBS=2 in memory and we have 128 GPUs available for training. This means with 4 gradient accumulation steps we’ll achieve our goal of 1024 samples or 4M tokens per training step. Now what if we suddenly have 512 GPUs available? We can achieve the same GBS and thus identical training by keeping MBS=2 and setting gradient accumulation steps to 1 and achieve faster training!</p>
|
| 586 |
|
| 587 |
-
<
|
| 588 |
-
|
|
|
|
|
|
|
|
|
|
|
|
|
| 589 |
|
| 590 |
<p>While data parallelism cleverly overlaps the all-reduce gradient synchronization with backward computation to save time, this benefit starts to break down at large scales. As we add more and more GPUs (hundreds or thousands), the overhead of coordinating between them grows significantly. The end result? We get less and less efficient returns from each additional GPU we add to the system:</p>
|
| 591 |
|
|
@@ -610,10 +640,10 @@
|
|
| 610 |
|
| 611 |
<p>In this section we will introduce DeepSpeed ZeRO (<strong>Ze</strong>ro <strong>R</strong>edundancy <strong>O</strong>ptimizer), a memory optimization technology designed to reduce memory redundancies in LLM training.</p>
|
| 612 |
|
| 613 |
-
<aside>We’ll focus on ZeRO-1 to ZeRO-3 in this blog as it should give a broad view on how it helps reduce memory while showing the tradeoffs to take into account. You can find more ZeRO flavors in the <a href="https://www.deepspeed.ai/tutorials/zero/">DeepSpeed docs</a>.</aside>
|
| 614 |
-
|
| 615 |
<p>While Data Parallelism is very efficient in scaling training, the naive replication of optimizer states, gradients, and parameters across each DP rank introduces a significant memory redundancy. ZeRO eliminates memory redundancy by partitioning the optimizer states, gradients, and parameters across the data parallel dimension, while still allowing computation with the full set of parameters. This sometimes requires more communications between DP ranks which may or may not be fully overlapped as we’ll see next!</p>
|
| 616 |
|
|
|
|
|
|
|
| 617 |
<p>This approach is organized into three possible optimization stage of ZeRO:</p>
|
| 618 |
|
| 619 |
<ul>
|
|
@@ -622,10 +652,10 @@
|
|
| 622 |
<li>ZeRO-3 (also called FSDP for “Fully-Sharded Data Parallelism”): optimizer state + gradient + parameter partitioning</li>
|
| 623 |
</ul>
|
| 624 |
|
| 625 |
-
<p>You might be missing the activations among the things we can shard. Since each DP replica of the model receives a different micro-batch the activations on each DP rank also differ so they are not duplicated and thus can’t be sharded!</p>
|
| 626 |
-
|
| 627 |
<aside>When we say partitioning, it means alongside the DP axis, as ZeRO is part of Data Parallelism. We’ll see later that we can partition alongside other axes.</aside>
|
| 628 |
|
|
|
|
|
|
|
| 629 |
<p>Let’s have a closer look how much we can save with the partitioning of each ZeRO stage!</p>
|
| 630 |
|
| 631 |
<h4>Memory usage revisited</h4>
|
|
@@ -639,7 +669,6 @@
|
|
| 639 |
<li>- Model’s gradients in fp32: <d-math>4\Psi</d-math> (optional, only accounted if we want to accumulate grads in fp32)</li>
|
| 640 |
</ul>
|
| 641 |
|
| 642 |
-
|
| 643 |
<p>If we don’t accumulate gradients in fp32 this gives us a total memory consumption of <d-math>2\Psi + 2\Psi + 12\Psi</d-math>, and if we accumulate it would be <d-math>2\Psi + 6\Psi + 12\Psi</d-math>. Let’s focus for now on the case without fp32 gradient accumulation for simplicity but you can just add the additional bytes to the gradient term which are affected by ZeRO-2 and 3.</p>
|
| 644 |
|
| 645 |
<p>The idea of ZeRO is to shard these objects across the DP ranks, each node only storing a slice of the items which are reconstructed when and if needed, thereby dividing memory usage by the data parallel degree <d-math>N_d</d-math>:</p>
|
|
@@ -683,7 +712,12 @@
|
|
| 683 |
<li>During forward: We can overlap the all-gather of each layer’s parameters with the forward pass.</li>
|
| 684 |
</ul>
|
| 685 |
|
| 686 |
-
<
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 687 |
|
| 688 |
<p>In ZeRO-1 the optimizer states have been partitioned, which means that each replica only updates <d-math>\frac{1}{N_d}</d-math> of the optimizer states. The keen reader must have noticed that there is no real need to have all gradients on all DP ranks in the first place since only a subset is needed for the optimization step. Meet ZeRO-2!</p>
|
| 689 |
|
|
@@ -709,7 +743,12 @@
|
|
| 709 |
|
| 710 |
<p>For Stage 3 we extend the above approach of sharding optimizer states and gradients over DP replicas up to sharding the model’s parameters.</p>
|
| 711 |
|
| 712 |
-
<
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 713 |
|
| 714 |
<p>So how do we do a forward or backward pass in practice if all parts of the model are distributed? Quite simply we gather them on-demand when we need them. In the forward pass this looks as follows:</p>
|
| 715 |
|
|
@@ -727,7 +766,7 @@
|
|
| 727 |
|
| 728 |
<p>In terms of memory we can see that our equation now reached it’s final form of <d-math>\frac{2\Psi +2\Psi+k\Psi}{N_d}</d-math> which means we can drive memory usage down indefinitely if we can increase the DP rank, at least for the model related parameters. Notice how it doesn’t help with the intermediate activations, for that we can use activation checkpointing and gradient accumulation as we’ve seen in earlier chapters.</p>
|
| 729 |
|
| 730 |
-
<aside>If you want to read more about FSDP1, FSDP2 and some of the implementation complexities around them, you should take some time to go over
|
| 731 |
|
| 732 |
<p><strong>Let’s summarize our journey into DP and ZeRO so far: we have seen that we can increase throughput of training significantly with DP, simply scaling training by adding more model replicas. With ZeRO we can train even models that would ordinarily not fit into a single GPU by sharding the parameters, gradients and optimizers states across DP, while incurring a small communications cost.
|
| 733 |
</strong></p>
|
|
@@ -834,8 +873,12 @@
|
|
| 834 |
|
| 835 |
<p>As we can see, increasing tensor parallelism reduces the memory needed for model parameters, gradients and optimizer states on each GPU. While tensor parallelism does help reduce activation memory in attention and feedforward layers by sharding the matrix multiplications across GPUs, we don't get the full memory benefits we could. This is because operations like layer normalization and dropout still require gathering the full activations on each GPU, partially negating the memory savings. We can do better by finding ways to parallelize these remaining operations as well.</p>
|
| 836 |
|
| 837 |
-
<
|
| 838 |
-
|
|
|
|
|
|
|
|
|
|
|
|
|
| 839 |
|
| 840 |
<p>This raises an interesting question - could we extend tensor parallelism to these remaining operations as well? Indeed, it's possible to parallelize layer norm, dropout and other operations too, which we'll explore next.</p>
|
| 841 |
|
|
@@ -845,7 +888,12 @@
|
|
| 845 |
|
| 846 |
<p>Rather than gathering the full hidden dimension on each GPU (which would defeat the memory benefits of TP), we can instead shard these operations along the sequence length dimension. This approach is called <strong>sequence parallelism (SP)</strong>.</p>
|
| 847 |
|
| 848 |
-
<
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 849 |
|
| 850 |
<p>Sequence parallelism (SP) involves splitting the activations and computations for the parts of the model not handled by tensor parallelism (TP) such as Dropout and LayerNorm, but along the input sequence dimension rather than across hidden dimension. This is needed because these operations require access to the full hidden dimension to compute correctly. For example, LayerNorm needs the full hidden dimension to compute mean and variance:</p>
|
| 851 |
|
|
@@ -1000,7 +1048,12 @@
|
|
| 1000 |
|
| 1001 |
<p>However, there are two limits to TP and SP: 1) if we scale the sequence length the activation memory will still blow up in the TP region and 2) if the model is too big to fit with TP=8 then we will see a massive slow-down due to the inter-node connectivity.</p>
|
| 1002 |
|
| 1003 |
-
<
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1004 |
|
| 1005 |
<p>We can tackle problem 1) with Context parallelism and problem 2) with Pipeline parallelism. Let’s first have a look at Context parallelism!</p>
|
| 1006 |
|
|
@@ -1028,7 +1081,12 @@
|
|
| 1028 |
|
| 1029 |
<p>That sounds very expensive if we do it naively. Is there a way to do this rather efficiently and fast! Thankfully there is: a core technique to handle this communication of key/value pairs efficiently is called <em>Ring Attention</em>.</p>
|
| 1030 |
|
| 1031 |
-
<
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1032 |
|
| 1033 |
<h3>Discovering Ring Attention</h3>
|
| 1034 |
|
|
@@ -1098,11 +1156,11 @@
|
|
| 1098 |
<p>In the TP section we saw that if we try to scale Tensor parallelism past the number of GPUs per single node (typically 4 or 8) we hit a lower bandwidth network called “inter-node connection” which can quite strongly impair our performances. We can see this clearly on e.g. the all-reduce operation when we perform it across several nodes:</p>
|
| 1099 |
|
| 1100 |
<p><img alt="image.png" src="/assets/images/placeholder.png" /></p>
|
| 1101 |
-
<p
|
| 1102 |
|
| 1103 |
<p>Sequence and context parallelism can help for long sequences but don’t help much if sequence length is not the root cause of our memory issues but rather the size of the model itself. For large model (70B+), the size of the weights alone can already push past the limits of the 4-8 GPUs on a single node. We can solve this issue by summoning the fourth (and last) parallelism dimension: “pipeline parallelism”.</p>
|
| 1104 |
|
| 1105 |
-
<p><img alt="image.png" src="/assets/images/placeholder.png" /></p
|
| 1106 |
|
| 1107 |
<p>Pipeline Parallelism is conceptually very simple –we’ll simply spread the layers of our model across GPUs – but the devil lies in implementing it efficiently. Let’s dive in it!</p>
|
| 1108 |
|
|
@@ -1337,8 +1395,15 @@
|
|
| 1337 |
<li>Context Parallelism primarily impacts attention layers since that's where cross-sequence communication is required, with other layers operating independently on sharded sequences.</li>
|
| 1338 |
<li>Expert Parallelism primarly affects the MoE layers (which replace standard MLP blocks), leaving attention and other components unchanged</li>
|
| 1339 |
</ul>
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1340 |
|
| 1341 |
-
<
|
| 1342 |
|
| 1343 |
<table>
|
| 1344 |
<thead>
|
|
@@ -1792,7 +1857,7 @@
|
|
| 1792 |
|
| 1793 |
<p>The meaning of the states can be found in the <a href="https://docs.nvidia.com/nsight-compute/ProfilingGuide/index.html#metrics-reference">Profiling Guide</a>, specifically in the <strong>Warp Stall Reasons</strong> section. There we can read that:</p>
|
| 1794 |
|
| 1795 |
-
<p><em><code>smsp__pcsamp_warps_issue_stalled_mio_throttle</code>: Warp was stalled waiting for the MIO (memory input/output) instruction queue to be not full. This stall reason is high in cases of extreme utilization of the MIO pipelines, which include special math instructions, dynamic branches, as well as shared memory instructions. When caused by shared memory accesses, trying to use fewer but wider loads can reduce pipeline pressure
|
| 1796 |
|
| 1797 |
<p>So it seems warps are stalling waiting for shared memory accesses to return ! To resolve this issue we can apply the <strong>Thread Coarsening</strong> technique by merging several threads into a single coarsened thread, we can significantly reduce shared memory accesses because each coarsened thread can handle multiple output elements which would increase the arithmetic intensity of the kernel.</p>
|
| 1798 |
|
|
|
|
| 222 |
<li>an optimization step using the gradients to update the parameters</li>
|
| 223 |
</ol>
|
| 224 |
|
| 225 |
+
<aside>As we’ll see later, these steps may be repeated or intertwined but for now we’ll start simple.</aside>
|
| 226 |
+
|
| 227 |
<p>It looks generally like this: </p>
|
| 228 |
<p><img alt="image.png" src="assets/images/placeholder.png" /></p>
|
| 229 |
|
|
|
|
|
|
|
| 230 |
<p>In this figure, the boxes on the top line can be seen as successive layers inside a model (same for the last line). The red boxes are the associated gradients for each of these layers, computed during the backward pass.</p>
|
| 231 |
|
| 232 |
<p>The batch size (<d-math>bs</d-math>) is one of the important hyper-parameters for model training and affects both model convergence and throughput.</p>
|
|
|
|
| 241 |
|
| 242 |
<p>In the simplest case, training on a single machine, the <d-math>bs</d-math> (in samples) and <d-math>bst</d-math> can be computed from the model input sequence length (seq) as follows :</p>
|
| 243 |
|
|
|
|
|
|
|
|
|
|
| 244 |
<d-math block>
|
| 245 |
bst=bs *seq
|
| 246 |
</d-math>
|
| 247 |
|
| 248 |
+
<p>From here onward we’ll show the formulas for the batch size in terms of samples but you can always get its token-unit counterpart by multiplying it with the sequence length.</p>
|
| 249 |
+
|
| 250 |
<p>A sweet spot for recent LLM training is typically on the order of 4-60 million tokens per batch. However, a typical issue when scaling the training of our model to these large batch sizes is out-of-memory issues, ie. our GPU doesn’t have enough memory.</p>
|
| 251 |
|
| 252 |
<aside>Note: Llama 1 was trained with a batch size of ~4M tokens for 1.4 trillions tokens while DeepSeek was trained with a batch size of ~60M tokens for 14 trillion tokens.
|
|
|
|
| 266 |
<li>Model gradients</li>
|
| 267 |
<li>Optimizer states</li>
|
| 268 |
</ul>
|
| 269 |
+
|
| 270 |
+
<div class="note-box">
|
| 271 |
+
<p class="note-box-title">📝 Note</p>
|
| 272 |
+
<p class="note-box-content">
|
| 273 |
+
You would think for a model you could compute the memory requirements exactly but there are a few additional memory occupants that makes it hard to be exact:
|
| 274 |
<ul>
|
| 275 |
<li>CUDA Kernels typically require 1-2 GB of GPU memory, which you can quickly verify by running <code>import torch; torch.ones((1, 1)).to("cuda")</code> and then checking the GPU memory with <code>nvidia-smi</code>.</li>
|
| 276 |
<li>Some rest memory usage from buffers, intermediate results and some memory that can’t be used due to fragmentation</li>
|
| 277 |
</ul>
|
| 278 |
+
We’ll neglect these last two contributors as they are typically small and constant factors.
|
| 279 |
+
</p>
|
| 280 |
+
</div>
|
| 281 |
|
| 282 |
<p>These items are stored as tensors which come in different <em>shapes</em> and <em>precisions</em>. The <em>shapes</em> are determined by hyper-parameters such as batch size, sequence length, model hidden dimensions, attention heads, vocabulary size, and potential model sharding as we’ll see later. <em>Precision</em> refers to formats like FP32, BF16, or FP8, which respectively require 4, 2, or 1 byte to store each single value in the tensor.</p>
|
| 283 |
|
|
|
|
| 332 |
\begin{aligned}
|
| 333 |
& m_{params} = 2 * N \\
|
| 334 |
& m_{grad} = 2 * N \\
|
| 335 |
+
& m_{params\_fp32} = 4 * N \\
|
| 336 |
& m_{opt} = (4+4) * N
|
| 337 |
\end{aligned}
|
| 338 |
</d-math>
|
| 339 |
|
| 340 |
+
<div class="note-box">
|
| 341 |
+
<p class="note-box-title">📝 Note</p>
|
| 342 |
+
<p class="note-box-content">
|
| 343 |
+
Some librarie store grads in fp32 which would require an additional <d-math>m_{params\_fp32} = 4 * N</d-math> memory. This is done for example in nanotron, because <code>bf16</code> is lossy for smaller values and we always prioritize stability. See <a href="https://github.com/microsoft/DeepSpeed/issues/1773">this DeepSpeed issue</a> for more information.
|
| 344 |
+
|
| 345 |
+
</p>
|
| 346 |
+
</div>
|
| 347 |
|
| 348 |
<p>Interestingly, mixed precision itself doesn’t save overall memory as it just distributes the memory differently across the three components, and in fact adds another 4 bytes over full precision training if we accumulate gradients in FP32. It’s still advantageous as having the model which does the forward/backward in half precision it allows us to (1) use optimized lower precision operations on the GPU which are faster and (2) reduces the activation memory requirements during the forward pass.</p>
|
| 349 |
|
|
|
|
| 431 |
|
| 432 |
<p><img alt="llama-8b-memory-bars--recomp.png" src="/assets/images/placeholder.png" /></p>
|
| 433 |
|
| 434 |
+
<div class="note-box">
|
| 435 |
+
<p class="note-box-title">📝 Note</p>
|
| 436 |
+
<p class="note-box-content">
|
| 437 |
+
When you’re measuring how efficient your training setup is at using the accelerator’s available compute, you may want to take recomputation into account when measuring the total FLOPS (Floating point operations per second) of your training setup and comparing it to theoretical maximum FLOPS of your GPU/TPU/accelerator to estimate GPU utilization. Taking recomputation into account when calculating FLOPS for a training step gives a value called “hardware FLOPS” which is the real number of operations performed on the accelerator. Dividing this number by the duration of one training step and the maximum accelerator FLOPS yields the <strong><em>Hardware FLOPS Utilization (HFU).</em></strong>
|
| 438 |
+
<br>
|
| 439 |
+
<br>
|
| 440 |
+
However, when comparing various accelerators together, what really matters at the end of the day is the start-to-end time needed to train the same models on the same dataset, ie. if an accelerator allows to skip recomputation and thus perform less operation per second for a faster training it should be rewarded. Thus, alternative is to compute what is called <strong><em>Model FLOPS Utilization (MFU)</em></strong>, which in contrast to HFU only accounts for the required operations to compute the forward+backward passes, and not recomputation, ie. is specific to the model, not the training implementation.
|
| 441 |
+
</p>
|
| 442 |
+
</div>
|
| 443 |
+
|
| 444 |
+
|
| 445 |
+
<aside> </aside>
|
| 446 |
|
| 447 |
+
<aside></aside>
|
| 448 |
|
| 449 |
<p>Most training frameworks these days use FlashAttention (which we’ll cover a bit later) which integrate natively activation recomputation in its optimization strategy by recomputing attention scores and matrices in the backward pass instead of storing them. Thus most people using Flash Attention are already making use of selective recomputation.</p>
|
| 450 |
|
|
|
|
| 476 |
|
| 477 |
<p><img alt="image.png" src="/assets/images/placeholder.png" /></p>
|
| 478 |
|
|
|
|
|
|
|
| 479 |
<aside>Using gradient accumulation means we need to keep buffers where we accumulate gradients which persist throughout a training step. Whereas without gradient accumulation, in the backward gradients are computed while freeing the activations memory, which means a lower peak memory.</aside>
|
| 480 |
|
| 481 |
+
<p><strong>Gradient accumulation allows us to reduce memory of activations which grow linearly with batch size by computing only only partial, micro-batches. There is a small overhead caused by the additional forward and backward passes.</strong></p>
|
| 482 |
+
|
| 483 |
+
|
| 484 |
<p>But if you’ve carefully followed, you probably noticed that the forward/backward passes for each micro-batch can actually be run in parallel. Forward/backward passes are independent from each other, with independent input samples being the only difference. Seems like it’s time to start extending our training to more than one GPU! </p>
|
| 485 |
|
| 486 |
<p>Let’s get a larger workstation 🖥️ with a couple of GPUs and start investigating our first scaling technique called <em><strong>data parallelism</strong> which is just a parallel version of gradient accumulation</em>.</p>
|
|
|
|
| 569 |
|
| 570 |
<p>In PyTorch, this is typically solved by adding a <a href="https://github.com/pytorch/pytorch/blob/5ea67778619c31b13644914deef709199052ee55/torch/nn/parallel/distributed.py#L1408-L1435"><code>model.no_sync()</code></a> decorator, which disables gradient synchronization, on the backward passes which don’t need reduction.</p>
|
| 571 |
|
| 572 |
+
<div class="note-box">
|
| 573 |
+
<p class="note-box-title">📝 Note</p>
|
| 574 |
+
<p class="note-box-content">
|
| 575 |
+
<p>When performing communication operations, tensors must be contiguous in memory. To avoid redundant memory copies during communication, ensure that tensors that will be communicated are stored contiguously in memory. Sometimes we need to allocate additional continuous buffers of the size of activations or model parameters specifically for communication, which contributes to the peak memory usage during training.
|
| 576 |
+
</p>
|
| 577 |
+
</div>
|
| 578 |
+
|
| 579 |
+
<p>Now that we combined both DP and gradient accumulation let's have a look what that means for the global batch size.</p>
|
| 580 |
|
| 581 |
<h3>Revisit global batch size</h3>
|
| 582 |
<p>Let’s update our batch size equation with our newly learned Data Parallelism and Gradient Accumulation parameters:</p>
|
|
|
|
| 603 |
<li>Finally, we determine the number of available GPUs for our target DP. The ratio of GBS to DP gives us the remaining number of gradient accumulation steps needed for the desired GBS. </li>
|
| 604 |
</ol>
|
| 605 |
|
| 606 |
+
<aside>For instance DeepSeek and Llama models are trained with a 4k tokens sequence length during the main pretraining phase.<br><br>The reason 2-8k work well for pretraining is that documents that are longer are very rare on the web. See this <a href="https://www.harmdevries.com/post/context-length/">Harm’s blogpost</a> for a detailed analysis.</aside>
|
| 607 |
|
|
|
|
|
|
|
| 608 |
|
| 609 |
<p>If the gradient accumulation ratio is lower than one, i.e. we have too many GPUs a.k.a GPU-rich 🤑 (!), we can either choose to not use all our GPUs, explore a larger global batch size or test if a lower MBS will speed up training. In the latter case we’ll end up prioritizing throughput over individual GPU compute efficiency, using a smaller MBS than possible in order to speed up training.</p>
|
| 610 |
|
| 611 |
<p>Time to take a concrete example: Let’s say we want to train a recent model with a GBS of 4M tokens and a sequence length of 4k. This means our batch size will be 1024 samples (we pick powers of two). We observe that a single GPU can only fit MBS=2 in memory and we have 128 GPUs available for training. This means with 4 gradient accumulation steps we’ll achieve our goal of 1024 samples or 4M tokens per training step. Now what if we suddenly have 512 GPUs available? We can achieve the same GBS and thus identical training by keeping MBS=2 and setting gradient accumulation steps to 1 and achieve faster training!</p>
|
| 612 |
|
| 613 |
+
<div class="note-box">
|
| 614 |
+
<p class="note-box-title">📝 Note</p>
|
| 615 |
+
<p class="note-box-content">
|
| 616 |
+
<p>Bear in mind that at the 512+ GPUs scale, depending on the network used, the communication operations will start to be bound by <em>ring latency</em> (time required for a signal to propagate once around the ring) which means we can no longer fully overlap the DP communications. This will decrease our compute efficiency and hit our throughput. In this case we should start exploring other dimensions to parallelize on.
|
| 617 |
+
</p>
|
| 618 |
+
</div>
|
| 619 |
|
| 620 |
<p>While data parallelism cleverly overlaps the all-reduce gradient synchronization with backward computation to save time, this benefit starts to break down at large scales. As we add more and more GPUs (hundreds or thousands), the overhead of coordinating between them grows significantly. The end result? We get less and less efficient returns from each additional GPU we add to the system:</p>
|
| 621 |
|
|
|
|
| 640 |
|
| 641 |
<p>In this section we will introduce DeepSpeed ZeRO (<strong>Ze</strong>ro <strong>R</strong>edundancy <strong>O</strong>ptimizer), a memory optimization technology designed to reduce memory redundancies in LLM training.</p>
|
| 642 |
|
|
|
|
|
|
|
| 643 |
<p>While Data Parallelism is very efficient in scaling training, the naive replication of optimizer states, gradients, and parameters across each DP rank introduces a significant memory redundancy. ZeRO eliminates memory redundancy by partitioning the optimizer states, gradients, and parameters across the data parallel dimension, while still allowing computation with the full set of parameters. This sometimes requires more communications between DP ranks which may or may not be fully overlapped as we’ll see next!</p>
|
| 644 |
|
| 645 |
+
<aside>We’ll focus on ZeRO-1 to ZeRO-3 in this blog as it should give a broad view on how it helps reduce memory while showing the tradeoffs to take into account. You can find more ZeRO flavors in the <a href="https://www.deepspeed.ai/tutorials/zero/">DeepSpeed docs</a>.</aside>
|
| 646 |
+
|
| 647 |
<p>This approach is organized into three possible optimization stage of ZeRO:</p>
|
| 648 |
|
| 649 |
<ul>
|
|
|
|
| 652 |
<li>ZeRO-3 (also called FSDP for “Fully-Sharded Data Parallelism”): optimizer state + gradient + parameter partitioning</li>
|
| 653 |
</ul>
|
| 654 |
|
|
|
|
|
|
|
| 655 |
<aside>When we say partitioning, it means alongside the DP axis, as ZeRO is part of Data Parallelism. We’ll see later that we can partition alongside other axes.</aside>
|
| 656 |
|
| 657 |
+
<p>You might be missing the activations among the things we can shard. Since each DP replica of the model receives a different micro-batch the activations on each DP rank also differ so they are not duplicated and thus can’t be sharded!</p>
|
| 658 |
+
|
| 659 |
<p>Let’s have a closer look how much we can save with the partitioning of each ZeRO stage!</p>
|
| 660 |
|
| 661 |
<h4>Memory usage revisited</h4>
|
|
|
|
| 669 |
<li>- Model’s gradients in fp32: <d-math>4\Psi</d-math> (optional, only accounted if we want to accumulate grads in fp32)</li>
|
| 670 |
</ul>
|
| 671 |
|
|
|
|
| 672 |
<p>If we don’t accumulate gradients in fp32 this gives us a total memory consumption of <d-math>2\Psi + 2\Psi + 12\Psi</d-math>, and if we accumulate it would be <d-math>2\Psi + 6\Psi + 12\Psi</d-math>. Let’s focus for now on the case without fp32 gradient accumulation for simplicity but you can just add the additional bytes to the gradient term which are affected by ZeRO-2 and 3.</p>
|
| 673 |
|
| 674 |
<p>The idea of ZeRO is to shard these objects across the DP ranks, each node only storing a slice of the items which are reconstructed when and if needed, thereby dividing memory usage by the data parallel degree <d-math>N_d</d-math>:</p>
|
|
|
|
| 712 |
<li>During forward: We can overlap the all-gather of each layer’s parameters with the forward pass.</li>
|
| 713 |
</ul>
|
| 714 |
|
| 715 |
+
<div class="note-box">
|
| 716 |
+
<p class="note-box-title">📝 Note</p>
|
| 717 |
+
<p class="note-box-content">
|
| 718 |
+
<p>Unfortunately these techniques are not straightforward to implement and require sophisticated use of hooks/bucketing. In practice we can just use ZeRO-3/FSDP implementation where the FSDPUnit is the entire model, more details about this later.
|
| 719 |
+
</p>
|
| 720 |
+
</div>
|
| 721 |
|
| 722 |
<p>In ZeRO-1 the optimizer states have been partitioned, which means that each replica only updates <d-math>\frac{1}{N_d}</d-math> of the optimizer states. The keen reader must have noticed that there is no real need to have all gradients on all DP ranks in the first place since only a subset is needed for the optimization step. Meet ZeRO-2!</p>
|
| 723 |
|
|
|
|
| 743 |
|
| 744 |
<p>For Stage 3 we extend the above approach of sharding optimizer states and gradients over DP replicas up to sharding the model’s parameters.</p>
|
| 745 |
|
| 746 |
+
<div class="note-box">
|
| 747 |
+
<p class="note-box-title">📝 Note</p>
|
| 748 |
+
<p class="note-box-content">
|
| 749 |
+
<p>This stage is also called FSDP (Fully Shared Data Parallelism) in PyTorch native implementation. We’ll just refer to ZeRO-3 in this blogpost but you can think of FSDP wherever you see it.
|
| 750 |
+
</p>
|
| 751 |
+
</div>
|
| 752 |
|
| 753 |
<p>So how do we do a forward or backward pass in practice if all parts of the model are distributed? Quite simply we gather them on-demand when we need them. In the forward pass this looks as follows:</p>
|
| 754 |
|
|
|
|
| 766 |
|
| 767 |
<p>In terms of memory we can see that our equation now reached it’s final form of <d-math>\frac{2\Psi +2\Psi+k\Psi}{N_d}</d-math> which means we can drive memory usage down indefinitely if we can increase the DP rank, at least for the model related parameters. Notice how it doesn’t help with the intermediate activations, for that we can use activation checkpointing and gradient accumulation as we’ve seen in earlier chapters.</p>
|
| 768 |
|
| 769 |
+
<aside>If you want to read more about FSDP1, FSDP2 and some of the implementation complexities around them, you should take some time to go over <a href="https://christianjmills.com/posts/mastering-llms-course-notes/conference-talk-012/">this nice blog</a>.</aside>
|
| 770 |
|
| 771 |
<p><strong>Let’s summarize our journey into DP and ZeRO so far: we have seen that we can increase throughput of training significantly with DP, simply scaling training by adding more model replicas. With ZeRO we can train even models that would ordinarily not fit into a single GPU by sharding the parameters, gradients and optimizers states across DP, while incurring a small communications cost.
|
| 772 |
</strong></p>
|
|
|
|
| 873 |
|
| 874 |
<p>As we can see, increasing tensor parallelism reduces the memory needed for model parameters, gradients and optimizer states on each GPU. While tensor parallelism does help reduce activation memory in attention and feedforward layers by sharding the matrix multiplications across GPUs, we don't get the full memory benefits we could. This is because operations like layer normalization and dropout still require gathering the full activations on each GPU, partially negating the memory savings. We can do better by finding ways to parallelize these remaining operations as well.</p>
|
| 875 |
|
| 876 |
+
<div class="note-box">
|
| 877 |
+
<p class="note-box-title">📝 Note</p>
|
| 878 |
+
<p class="note-box-content">
|
| 879 |
+
<p>One interesting note about layer normalization in tensor parallel training - since each TP rank sees the same activations after the all-gather, the layer norm weights don't actually need an all-reduce to sync their gradients after the backward pass. They naturally stay in sync across ranks. However, for dropout operations, we must make sure to sync the random seed across TP ranks to maintain deterministic behavior.
|
| 880 |
+
</p>
|
| 881 |
+
</div>
|
| 882 |
|
| 883 |
<p>This raises an interesting question - could we extend tensor parallelism to these remaining operations as well? Indeed, it's possible to parallelize layer norm, dropout and other operations too, which we'll explore next.</p>
|
| 884 |
|
|
|
|
| 888 |
|
| 889 |
<p>Rather than gathering the full hidden dimension on each GPU (which would defeat the memory benefits of TP), we can instead shard these operations along the sequence length dimension. This approach is called <strong>sequence parallelism (SP)</strong>.</p>
|
| 890 |
|
| 891 |
+
<div class="note-box">
|
| 892 |
+
<p class="note-box-title">📝 Note</p>
|
| 893 |
+
<p class="note-box-content">
|
| 894 |
+
<p>The term Sequence Parallelism is a bit overloaded: the Sequence Parallelism in this section is tightly coupled to Tensor Parallelism and applies to dropout and layer norm operation. However, when we will move to longer sequences the attention computation will become a bottleneck, which calls for techniques such as Ring-Attention, which are sometimes also called <em>Sequence Parallelism</em> but we’ll refer to them as <em>Context Parallelism</em> to differentiate the two approaches. So each time you see sequence parallelism, remember that it is used together with tensor parallelism (in contrast to context parallelism, which can be used independently).
|
| 895 |
+
</p>
|
| 896 |
+
</div>
|
| 897 |
|
| 898 |
<p>Sequence parallelism (SP) involves splitting the activations and computations for the parts of the model not handled by tensor parallelism (TP) such as Dropout and LayerNorm, but along the input sequence dimension rather than across hidden dimension. This is needed because these operations require access to the full hidden dimension to compute correctly. For example, LayerNorm needs the full hidden dimension to compute mean and variance:</p>
|
| 899 |
|
|
|
|
| 1048 |
|
| 1049 |
<p>However, there are two limits to TP and SP: 1) if we scale the sequence length the activation memory will still blow up in the TP region and 2) if the model is too big to fit with TP=8 then we will see a massive slow-down due to the inter-node connectivity.</p>
|
| 1050 |
|
| 1051 |
+
<div class="note-box">
|
| 1052 |
+
<p class="note-box-title">📝 Note</p>
|
| 1053 |
+
<p class="note-box-content">
|
| 1054 |
+
<p>Since LayerNorms in the SP region operate on different portions of the sequence, their gradients will differ across TP ranks. To ensure the weights stay synchronized, we need to allreduce their gradients during the backward pass, similar to how DP ensures weights stay in sync. This is a small communication overhead since LayerNorm has relatively few parameters.
|
| 1055 |
+
</p>
|
| 1056 |
+
</div>
|
| 1057 |
|
| 1058 |
<p>We can tackle problem 1) with Context parallelism and problem 2) with Pipeline parallelism. Let’s first have a look at Context parallelism!</p>
|
| 1059 |
|
|
|
|
| 1081 |
|
| 1082 |
<p>That sounds very expensive if we do it naively. Is there a way to do this rather efficiently and fast! Thankfully there is: a core technique to handle this communication of key/value pairs efficiently is called <em>Ring Attention</em>.</p>
|
| 1083 |
|
| 1084 |
+
<div class="note-box">
|
| 1085 |
+
<p class="note-box-title">📝 Note</p>
|
| 1086 |
+
<p class="note-box-content">
|
| 1087 |
+
<p>Context Parallelism shares some conceptual similarities with Flash Attention (see later for more details) - both techniques rely on online softmax computation to reduce memory usage. While Flash Attention focuses on optimizing the attention computation itself on a single GPU, Context Parallelism achieves memory reduction by distributing the sequence across multiple GPUs.
|
| 1088 |
+
</p>
|
| 1089 |
+
</div>
|
| 1090 |
|
| 1091 |
<h3>Discovering Ring Attention</h3>
|
| 1092 |
|
|
|
|
| 1156 |
<p>In the TP section we saw that if we try to scale Tensor parallelism past the number of GPUs per single node (typically 4 or 8) we hit a lower bandwidth network called “inter-node connection” which can quite strongly impair our performances. We can see this clearly on e.g. the all-reduce operation when we perform it across several nodes:</p>
|
| 1157 |
|
| 1158 |
<p><img alt="image.png" src="/assets/images/placeholder.png" /></p>
|
| 1159 |
+
<p>Inter-node communication bandwidth measurements across different node counts, showing median (lines) and 5th-95th percentile ranges (shaded areas) for AllReduce, AllGather and ReduceScatter operations.</p>
|
| 1160 |
|
| 1161 |
<p>Sequence and context parallelism can help for long sequences but don’t help much if sequence length is not the root cause of our memory issues but rather the size of the model itself. For large model (70B+), the size of the weights alone can already push past the limits of the 4-8 GPUs on a single node. We can solve this issue by summoning the fourth (and last) parallelism dimension: “pipeline parallelism”.</p>
|
| 1162 |
|
| 1163 |
+
<p><img alt="image.png" src="/assets/images/placeholder.png" /></p>
|
| 1164 |
|
| 1165 |
<p>Pipeline Parallelism is conceptually very simple –we’ll simply spread the layers of our model across GPUs – but the devil lies in implementing it efficiently. Let’s dive in it!</p>
|
| 1166 |
|
|
|
|
| 1395 |
<li>Context Parallelism primarily impacts attention layers since that's where cross-sequence communication is required, with other layers operating independently on sharded sequences.</li>
|
| 1396 |
<li>Expert Parallelism primarly affects the MoE layers (which replace standard MLP blocks), leaving attention and other components unchanged</li>
|
| 1397 |
</ul>
|
| 1398 |
+
|
| 1399 |
+
<div class="note-box">
|
| 1400 |
+
<p class="note-box-title">📝 Note</p>
|
| 1401 |
+
<p class="note-box-content">
|
| 1402 |
+
<p>This similarity between EP and DP in terms of input handling is why some implementations consider Expert Parallelism to be a subgroup of Data Parallelism, with the key difference being that EP uses specialized expert routing rather than having all GPUs process inputs through identical model copies.
|
| 1403 |
+
</p>
|
| 1404 |
+
</div>
|
| 1405 |
|
| 1406 |
+
<p>TODO: the text between the table and figueres is still a bit sparse.</p>
|
| 1407 |
|
| 1408 |
<table>
|
| 1409 |
<thead>
|
|
|
|
| 1857 |
|
| 1858 |
<p>The meaning of the states can be found in the <a href="https://docs.nvidia.com/nsight-compute/ProfilingGuide/index.html#metrics-reference">Profiling Guide</a>, specifically in the <strong>Warp Stall Reasons</strong> section. There we can read that:</p>
|
| 1859 |
|
| 1860 |
+
<p><em><code>"smsp__pcsamp_warps_issue_stalled_mio_throttle</code>: Warp was stalled waiting for the MIO (memory input/output) instruction queue to be not full. This stall reason is high in cases of extreme utilization of the MIO pipelines, which include special math instructions, dynamic branches, as well as shared memory instructions. When caused by shared memory accesses, trying to use fewer but wider loads can reduce pipeline pressure."</em></p>
|
| 1861 |
|
| 1862 |
<p>So it seems warps are stalling waiting for shared memory accesses to return ! To resolve this issue we can apply the <strong>Thread Coarsening</strong> technique by merging several threads into a single coarsened thread, we can significantly reduce shared memory accesses because each coarsened thread can handle multiple output elements which would increase the arithmetic intensity of the kernel.</p>
|
| 1863 |
|
src/style.css
CHANGED
|
@@ -334,4 +334,39 @@ d-contents nav > ul > li > a:hover {
|
|
| 334 |
#graph svg rect {
|
| 335 |
cursor: pointer;
|
| 336 |
}
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 337 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 334 |
#graph svg rect {
|
| 335 |
cursor: pointer;
|
| 336 |
}
|
| 337 |
+
.note-box {
|
| 338 |
+
background-color: #f6f8fa;
|
| 339 |
+
border-left: 4px solid #444444;
|
| 340 |
+
padding: 1rem;
|
| 341 |
+
margin: 1rem 0; /* Keep this modest margin */
|
| 342 |
+
border-radius: 6px;
|
| 343 |
+
/* Add this to ensure the box only takes up needed space */
|
| 344 |
+
display: inline-block;
|
| 345 |
+
width: 100%;
|
| 346 |
+
}
|
| 347 |
+
|
| 348 |
+
.note-box-title {
|
| 349 |
+
margin: 0;
|
| 350 |
+
color: #444444;
|
| 351 |
+
font-weight: 600;
|
| 352 |
+
}
|
| 353 |
|
| 354 |
+
.note-box-content {
|
| 355 |
+
margin-top: 0.5rem;
|
| 356 |
+
margin-bottom: 0; /* Ensure no bottom margin */
|
| 357 |
+
color: #24292f;
|
| 358 |
+
}
|
| 359 |
+
|
| 360 |
+
/* For dark mode support */
|
| 361 |
+
@media (prefers-color-scheme: dark) {
|
| 362 |
+
.note-box {
|
| 363 |
+
background-color: #1c1c1c;
|
| 364 |
+
border-left-color: #888888;
|
| 365 |
+
}
|
| 366 |
+
.note-box-title {
|
| 367 |
+
color: #888888;
|
| 368 |
+
}
|
| 369 |
+
.note-box-content {
|
| 370 |
+
color: #d4d4d4;
|
| 371 |
+
}
|
| 372 |
+
}
|