README.md

metadata

title: ISCO-08 Hierarchical Accuracy Measure
datasets:
  - ICILS/multilingual_parental_occupations
tags:
  - evaluate
  - metric
description: >-
  The ISCO-08 Hierarchical Accuracy Measure is an implementation of the measure
  described in [Functional Annotation of Genes Using Hierarchical Text
  Categorization](https://www.researchgate.net/publication/44046343_Functional_Annotation_of_Genes_Using_Hierarchical_Text_Categorization)
  (Kiritchenko, Svetlana and Famili, Fazel. 2005) applied to the ISCO-08
  classification scheme by the International Labour Organization.
sdk: gradio
sdk_version: 4.36.1
app_file: app.py
pinned: false

Metric Card for ISCO-08 Hierarchical Accuracy Measure

Metric Description

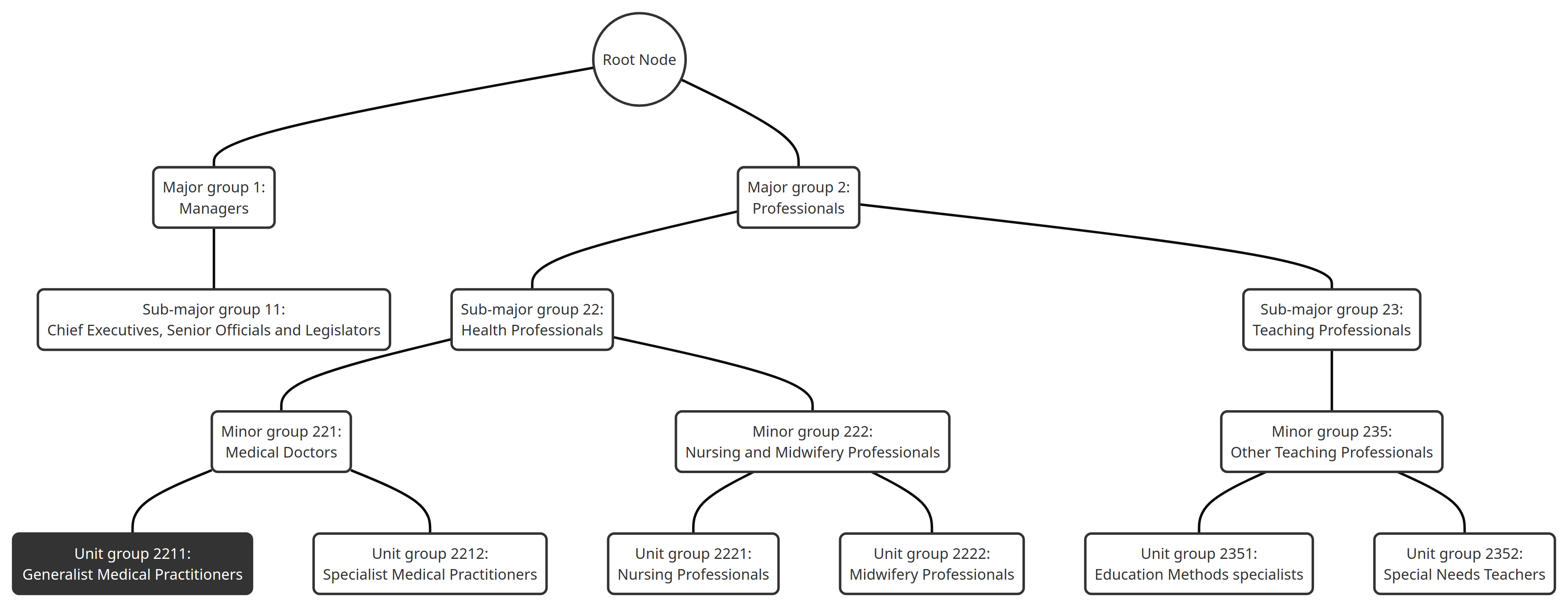
The hierarchical structure of the ISCO-08 classification scheme, as depicted in the Figure 1, is organized into four levels, delineated by the specificity of their codes:

Digits	Group level
1-digit	Major groups
2-digits	Sub-major groups
3-digits	Minor groups
4-digits	Unit groups

Figure 1: Hierarchical structure of the ISCO-08 classification scheme

In this context, the hierarchical accuracy measure is specifically designed to evaluate classifications within this structured framework. It emphasizes the importance of precision in classifying occupations at the correct level of specificity:

1. Major Groups (1-digit codes): The broadest category that encompasses a wide range of occupations grouped based on their fundamental characteristic and role in the job market. Misclassification among different Major groups implies a fundamental misunderstanding of the occupational role.

2. Sub-major Groups (2-digit codes): Provide a more detailed classification within each Major group, delineating categories that share specific occupational characteristics. Errors within a Major group but across different Sub-major groups are less severe than those across Major groups but are still significant due to the deviation from the correct occupational category.

3. Minor Groups (3-digit codes): Offer further granularity within Sub-major groups, classifying occupations that require similar skill sets and qualifications. Misclassifications within a Sub-major group but across different Minor groups are penalized, yet to a lesser extent than errors across Sub-major or Major groups, as they still fall within a broader correct occupational category.

4. Unit Groups (4-digit codes): The most specific level, identifying precise occupations. Misclassification within a Minor group, between different Unit groups, represents the least severe error, as it occurs within the context of closely related occupations.

The hierarchical accuracy measure rewards more precise classifications that correctly identify an occupation's placement down to the specific Unit group level and applies penalties for misclassifications based on the hierarchical distance between the correct and assigned categories. This approach allows for a refined evaluation of classification systems, acknowledging partially correct classifications while penalizing inaccuracies more severely as they deviate further from the correct level in the hierarchical structure.

For example, a misclassification into Unit group 2211 (Generalist Medical Practitioners) when the correct category is Unit group 2212 (Specialist Medical Practitioners) should incur a lesser penalty than misclassification into Unit group 2352 (Special Needs Teachers), as Unit groups 2211 and 2212 are within the same Minor group 221 (Medical doctors) and share a closer hierarchical relationship compared to Minor group 235 (Other teaching professionals) which is in a different Sub-major group (23 Teaching professionals).

The measure applies a higher penalty for errors that occur between more distant categories within the hierarchy:

1. Correct classifications at a more specific level (e.g., Minor group 2211) are evaluated more favorably than classifications at a more general level within the same hierarchy (e.g., Sub-major group 22), since the former indicates a closer match to the correct category.
2. Conversely, incorrect classifications at a more specific level are penalized more heavily than those at a more general level. For instance, classifying into Minor group 222 (Nursing and Midwifery Professionals) is considered worse than classifying into its parent category, Sub-major group 22, if the correct classification is Minor group 221, because the incorrect specific classification indicates a farther deviation from the correct category.

Misclassification among sibling categories (e.g., between different Minor groups within the same Sub-major group) is less severe than misclassification at a higher hierarchical level (e.g., between different Major groups).

The measure extends the concepts of precision and recall into a hierarchical context, introducing hierarchical precision ($hP$) and hierarchical recall ($hR$). In this framework, each sample belongs not only to its designated class but also to all ancestor categories in the hierarchy, excluding the root (we exclude the root of the graph, since all samples belong to the root by default). This adjustment allows the measure to account for the hierarchical structure of the classification scheme, rewarding more accurate location of a sample within the hierarchy and penalizing errors based on their hierarchical significance.

To calculate the hierarchical measure, we extend the set of real classes $C_i = {G}$ with all ancestors of class $G:\vec{C}_i = {B, C, E, G}$.

We also extend the set of predicted classes $C^′_i = {F}$ with all ancestors of class $F : \vec{C}^′_i = {C, F}$.

So, class $C$ is the only correctly assigned label from the extended set:$| \vec{C}_i ∩ \vec{C}^′_i| = 1$.

There are $| \vec{C}^′_i| = 2$ assigned labels and $| \vec{C}_i| = 4$ real classes.

Therefore, we get:

$hP = \frac{| \vec{C}_i ∩ \vec{C}^′_i|} {|\vec{C}^′_i |} = \frac{1}{2}$

$hR = \frac{| \vec{C}_i ∩ \vec{C}^′_i|} {|\vec{C}_i |} = \frac{1}{2}$

We also can combine the two values $hP$ and $hR$ into one hF-measure:

$$h{F}_{\beta }=\frac{({\beta }^2+1)\cdot hP\cdot hR}{({\beta }^2\cdot hP+hR)},\beta \in [0,+\mathrm{\infty })hF\_\beta \; =\; \backslash frac\{(\beta ^2\; +\; 1)\; ·\; hP\; ·\; hR\}\{(\beta ^2\; ·\; hP\; +\; hR)\},\; \beta \; \in \; [0,\; +\infty )$$

How to Use

Give general statement of how to use the metric

Provide simplest possible example for using the metric

TBA

Inputs

List all input arguments in the format below

• input_field (type): Definition of input, with explanation if necessary. State any default value(s).
• references (List[str]): List of reference ISCO-08 codes (true labels). This is the ground truth.
• predictions (List[str]): List of predicted ISCO-08 codes (predicted labels). This is the predicted classification or classification to compare against the ground truth.

Output Values

Explain what this metric outputs and provide an example of what the metric output looks like. Modules should return a dictionary with one or multiple key-value pairs, e.g. {"bleu" : 6.02}

Example output:

{
    "accuracy": 0.25,
    "hierarchical_precision": 1.0,
    "hierarchical_recall": 0.4,
    "hierarchical_fmeasure": 0.5714285714285715,
}

Values are decimal numbers between 0 and 1. Higher scores are better.

Values from Popular Papers

Give examples, preferrably with links to leaderboards or publications, to papers that have reported this metric, along with the values they have reported.

TBA

Examples

Give code examples of the metric being used. Try to include examples that clear up any potential ambiguity left from the metric description above. If possible, provide a range of examples that show both typical and atypical results, as well as examples where a variety of input parameters are passed.

def compute_metrics(p: EvalPrediction):
    preds = p.predictions[0] if isinstance(p.predictions, tuple) else p.predictions
    preds = np.argmax(preds, axis=1)
    # Use labels instead of ids for hierarchical ISCO-08 classification
    preds = [model.config.id2label[p] for p in preds]
    refs = [model.config.id2label[r] for r in p.label_ids]
    result = metric.compute(predictions=preds, references=refs)
    return result

More TBA

Limitations and Bias

Note any known limitations or biases that the metric has, with links and references if possible.

TBA

Citation

Cite the source where this metric was introduced.

TBA

Further References

Add any useful further references.

TBA